Fizikte dayanıklılık bir katı cismin özelliklerini kaybetmeden basma, germe ya da sıkıştırma gibi etkilere karşı gösterdiği dirençtir. Basmak, germek ya da sıkıştırmak kuvvet uygulamak demektir. Katı bir cisme kuvvet uygularsanız şeklini değiştirebilirsiniz. Şekli değişen cisim kuvveti kaldırdığınızda eski şeklini tekrar alır, buna esneklik denir. Örneğin, bir gitar telini gererseniz boyu uzar, esner. Teli gevşetirseniz tekrar eski haline döner. Ancak uyguladığınız kuvvet belli bir eşik değerini aşarsa, cismin esneklik özelliği kaybolur, şekli kalıcı olarak bozulur ya da cisim parçalanır. Dayanıklılık bir katı cismin üzerine uygulanan kuvvete esnekliği bozulmadan ya da parçalanmadan ne kadar dayanabileceği anlamına gelir. Bir başka örnek de binaların taşıyıcı kolonlarıdır, bu kolonlar binanın ağırlığını taşır ve dayanıklı olmaları gerekir. Kolonların kesit alanı ne kadar büyükse dayanıklılığı o kadar büyük olur.
Katı cisimler için dayanıklılık cismin kesit alanın cisme uygulanan kuvvete oranıdır. Dayanıklılık formülü şöyledir:
DAYANIKLILIK \alpha \frac{kesit \space alan}{kuvvet}
Bu konu anlatımında 9. sınıf fizik dersi kazanımlarına uygun olması için dayanıklılıktan bahsederken kuvveti doğrudan kullanmayacağız. Cisimlerin kendi ağırlıklarına karşı gösterdikleri dayanıklılık odağımız olacak. Cisimlerin ağırlığının kütleleriyle doğru orantılı olduğunu biliyoruz. Türdeş (homojen) bir cismin özkütlesinin de cismin her yerinde aynı olduğunu kabul ediyoruz. Bu nedenle türdeş cisimlerin kütlesinin hacimleriyle doğru orantılı olduğunu da söyleyebiliriz. Dayanıklılık oranlarını (formüllerini) kullanırken türdeş katı cisimlerin hacimleriyle kesit alanları arasındaki ilişkiyi inceleyeceğiz. Özetlersek:
G=mg m=d \times V DAYANIKLILIK = \frac{kesit \space alan}{G} DAYANIKLILIK = \frac{kesit \space alan}{d \times V \times g} DAYANIKLILIK \space \alpha \frac{kesit \space alan}{V (hacim)}Artık neden dayanıklılığı incelerken hacmin kesit alana oranıyla ilgilendiğimizi öğrendiğimize göre sırayla düzgün geometrik cisimlerin dayanıklılığına bakabiliriz. Sırasıyla dayanıklılık formüllerini inceleyelim.
Düzgün geometrik şekilli katı cisimlerin dayanıklılık oranları ve formülleri
Şekilleri düzgün olmayan cisimlerin dayanıklılığını hesaplamak oldukça zordur. Bu nedenle biz düzgün geometrik şekilli katı cisimlerin dayanıklılıklarını inceleyeceğiz.
Küp
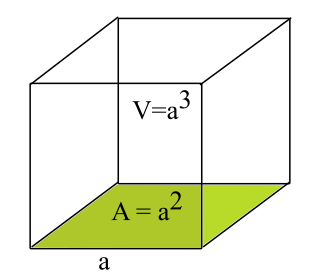
Bir ayrıtının uzunluğu a olan küpün kesit alanının hacmine oranı yani dayanıklılık formülü şöyledir:
Kesit alanı (A) = a x a = a2
Hacim (V) = a x a x a = a3
DAYANIKLILIK \space \alpha \frac{A}{V} DAYANIKLILIK \space \alpha \frac{a^2}{a^3} = \frac{1}{a}Küpün ayrıt uzunluğu iki katına çıkarsa dayanıklılığı yarıya iner. Üç katına çıkarsa, üçte birine iner. Küp için dayanıklılık ayrıt uzunluğuyla ters orantılıdır.
Dikdörtgenler prizması
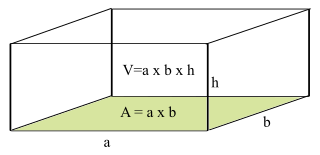
Bir ayrıtı a, diğer ayrıtı b, yüksekliği h olan bir dikdörtgenler prizmasının kesit alanının hacmine oranı bir başka deyişle dayanıklılığının formülü şöyle bulunur:
A = a x b
V = a x b x h
DAYANIKLILIK \space \alpha \frac{\cancel{a} \times \cancel{b}}{\cancel{a} \times \cancel{b} \times h} = \frac{1}{h}Dikdörtgenler prizması için dayanıklık yükseklikle ters orantılıdır, yükseklik arttıkça azalır.
Silindir
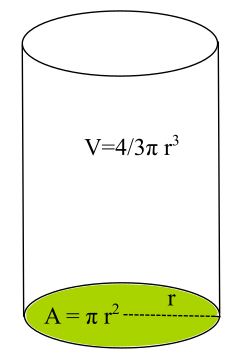
Taban yarıçapının uzunluğu r yüksekliği h olan bir silindirin kesit alanının hacmine oranı, silindirin dayanıklılık formülü:
A = πr2
V=πr2h
DAYANIKLILIK \space \alpha \frac{\cancel{\pi} \times \cancel{r^2}}{\cancel{\pi} \times \cancel{r^2} \times h} = \frac{1}{h}
Silindir için dayanıklık yükseklikle ters orantılıdır.
Küre
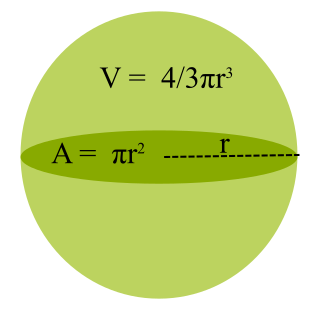
Yarıçapının uzunluğu r olan bir kürenin kesit alanının hacmine oranı yani kürenin dayanıklılık formülü:
A = πr2
V = \frac{4}{3}\pi r^3 DAYANIKLILIK \space \alpha \frac{\pi r^2}{\frac{4}{3}\pi r^3} = \frac{3}{4r}Kürenin dayanıklılığı yarıçapıyla ters orantılıdır. Başındaki sabit 3/4 önemli değil, değişken olan yarıçap. Kürenin yarıçapı arttıkça dayanıklılığı azalır.
Dayanıklılık ile ilgili sonuçlar
İncelediğimiz düzgün geometrik şekillerin tümünde dayanıklılığın bir göstergesi olan kesit alanın hacme oranının boyutlar büyüdükçe azaldığını gördük. Örneğin, dikdörtgenler prizması şeklinde binaları karşılaştırırsak, aynı taban alanına sahip iki binadan yüksek olanın daha az dayanıklı olduğu sonucuna varabiliriz. Gökdelenlerin belli bir yüksekliği aşamamalarının nedeni dayanıklılığın yükseklikle birlikte azalmasıdır.
Gelileo aynı yükseklikten düşen bir atın kemiklerinin kırıldığını ama bir köpeğin kemiklerinin kırılmadığını gözlemiş. Bizim dayanıklılığın göstergesi olarak kullandığımız kesit alanının hacme oranının, büyüklüğe göre azaldığı sonucuna varmış. Buna kare küp kanunu demiş, yani boyutun karesinin küpüne oranı.
Böcekler gibi küçük canlıların kendi ağırlıklarının çok daha fazlasını taşıyabilmelerinin nedeni kesit alanlarının hacimlerine oranının büyük olmasıdır. Boyutlar büyüdükçe bu oran azalır, dayanıklılık da azalır. Gergedan gibi büyük canlılar bu nedenle kendi ağırlıklarını bile ancak taşıyabilirler.
Eğer bir karınca bir inek kadar büyüseydi kendi ağırlığını taşıyabilir miydi? Peki ya King Kong gerçek olabilir mi? 20 metre boyunda bir goril gerçekten fiziksel olarak var olabilir mi? Yorumlarda cevaplarınızı bekliyorum.
Örnek soru – bir ipin dayanıklılığı
Yarıçapı 2 cm olan bir ip kopmadan en çok 100 N yük taşıyabilmektedir. Bu ipin yarıçapı 4 cm’ye çıkarılırsa en çok kaç N ağırlık taşıyabilir?
Çözüm:
Dayanıklılık için mutlaka kesit alanın hacme oranını kullanmak zorunda değiliz. Hatta bu soruda kesinlikle kullanamayız. Dayanıklılığın asıl tanımını kullanmak zorundayız. İpin sabit bir dayanıklılığı olduğunu kabul ediyoruz. Dayanıklılık formülünü hatırlayalım:
DAYANIKLILIK = \frac{kesit \space alan}{kuvvet} DAYANIKLILIK{ip} = \frac{\pi (2 \space cm \times 2 \space cm)}{100 \space N} = \frac{\pi (4 \space cm \times 4 \space cm)}{F} F = \frac{4^2 \times 100}{2^2} = \frac{16 \times 100 \space N}{4} DAYANIKLILIK{ip} = 400 \space Nİp ya da halat dayanıklılığı problemlerinde bu sorudaki çözüm yöntemimiz işinize yarayabilir.
Dayanıklılık ile ilgili Fizik dersi Kazanımları
9.2.2.1. Dayanıklılık kavramını açıklar.
- Düzgün geometrik şekilli cisimlerden küp, dikdörtgenler prizması, silindir ve kürenin kesit alanının hacme oranı dışında dayanıklılık kavramı ile ilgili matematiksel hesaplamalara girilmez.
Dayanıklılık için mutlaka kesit alanın hacme oranını kullanmak zorunda değiliz. Hatta bu soruda kesinlikle kullanamayız.
İşte aradığım ifade teşekkürler
Bulduğuna sevindim Burak.
4Pixr kare 100N taşıyorsa.
Aynı boydaki 16pixr kare 400N taşır.
dayanıklılık sabit demeye bile gerek yok hocam.
Aynı ip aynı boy yeterli.
Hocam merhaba.Öncelikle yazınız için teşekkür ederim. Benim sorum dinazorlarla ilgili olucak. Daha önceki okuduğum birkaç fizik makalesinde dinazorların varolamayacağı, bunun nedenininde dayanıklılık ilkesiyle çeliştiğiydi. Sizin bu konuda bir bilginiz var mı acaba
Filler var mı var? Dinazor neden olmasın?
bence olur neden şu bakımdan olur şimdi bi geçmişe gidelim dinozrların olduğu dönemlere ve bizim döemimizi karşılaştıralım.Bizim dönemimizde fil zürafa gibi canlılar var ve insan oğlunun boyu 190cm fln olsun (hastalıklar var ama onlar sayılmaz) geçmişte ise dinozorlar var etobur otobur ve hepçil vb. ve insan oğlunun boyu bizim nesile göre en küçük insan 200cm bu demek oluyoki dinozor ve filler arasında hiçbir fark yok.UMARIM FAYDALI OLMUŞTUR :D…
Hocamızın müsadesiyle,misafir fizik öğretmeni olarak bu soruya bende cevap vermek istedim.Harika bir soru.
Dinozorlar için hiç duymadım ama devler için mümkün değil diye geçer.
Devler insan formunda gibi düşünürüz. Aynı kas yapısı, kemik yoğunluğu vb.
gerçekte de böyle,troit bezinin fazla çalışmasından oluşan devlik sendromu olan kişiler kendi ağırlığının altında ezilir.Karaya vuran balınalar boğulmadan kemikleri kırılarak hayatını kaybeder.
Özetle;canlı bu boyutlara ulaşabiliyor ve dayanıklılık formülünü altüst ediyorsa kas yapısını ona göre evrimleştirmiş demektir.(Biyoloji ve katıhal fiziği )
Yani;2 kat yaparken 2 ton demir kullandıysak 4 kat yaparken 4 ton demir kullanmayacağız. Veya demir değil daha dayanıklı bir materyal kullanacağız.
Yazınız çok faydı oldu teşekkür ederim.
Hocam çok teşekkürler, ancak dayanıklılıkta k sabitini yazmamanız yanıltıcı oluyor. Halatlarda da uç uca bağlanmış halatları bu bilgilerle çözemedim formülü en net haliyle paylaşır mısınız?
Yararlı oldu, teşekkürler.
Hangisinin dayanıklılığı daha fazladır uğur böceği (U). Boğa (B). Tavşan(T). Dayanıklılığı büyük olandan küşük olana sıralarmısınız.
U>T>B olur.
Bir gorili aynı oranda büyütürsek muhtemelen kemikleri o an parçalanırdı. Çünkü kesit alanı a^2 artarken hacim a^3 olarak artış gösterir. Yani artış miktarı daha fazladır.
Faydalı olmuş bravo düşünceli yapınızı tebrik ederim.
selamun aleykum hocam bu yazdığınız dayanıklılık konusu bana performans olarak geldi bunun hepsini yazmak zorunda kaldım neden ‘FİZİK’ bu kadar zor bunu bana açıklayın ilk sınav 63 geldi inşallah 40 üstü alırım
MERHABA BEN FİZİK HOCASİ ÇOK İYİ KONULAR SİNAVDA AYNOSİ ÇIKACAK
Dayanıklılığın yüzey alanı ile bir bağlantısı var mıdır
Hocam elinize sağlık, ancak cevap 385 değil 400 yuvarlamadan kaynaklı bir hata var orada.
taşıyabileceği yük miktarı kesit alanı ile D. O. lıdır. formül yazmaya gerek yoktur. 2 nin karesi 4, 100 N taşırsa; 4 ün karesi 16 100’ün 4 katı yük taşır. oda 400 N olur.
bir karınca eğer inek boyunda olsaydı kendisini taşıyabilir ne de olsa ayaklarıda büyüyor.King Kong da var olsaydı kendisin rahatlıkla taşırdı bence ayakları her yere vuruşunda yere gömülürdü o akdar ağırlığı taşıyabiliceğini sanmıyorum bence yaşayabilirdi neden olmasın biz nasıl yaşıyo isek onlarda yaşayabilir.(BENCE)
kesit alanı bölü hacim ile dayanıklılık aynıdır diyoruz evet en dayanıklı cisim olarak küreyi söylüyoruz ama aynı hacim de kesit alanı en küçük olan küredir yani bu durumda oran da en küçük kürenin oluyo anlamadım
Hocam bir şey soracağım ipin kesit alanını nasıl hesapladınız orda kafam karıştı cevaplarsanız sevinirim 🙂
İpi bir silindir olarak modelledik. Silindirin kesit alanı bir daire olduğu için pi*r^2.
Dayanıklılık formülü MEB kitabında net değil. Bi agirlik bi hacim kullanıyor neden olduğunu da söylemiyor. Bu sayfada netleşti. Teşekkürler.
Kürenin dayanıklılığı neden en fazla
Hacminin kesit alanına oranı geometrisinden dolayı böyle çıktığı için.
Hocam o zaman ipin dayanıklılığını her zaman aynı mı kabul ediyoruz sadece taşıyacağı yük artabiliyor?
İpin dayanıklılığı yarıçapına göre değişiyor. Yarıçap artarsa artıyor. Eğer değişmezse taşıyacağı azami yük dayanıklılıktan hesaplanıyor ve değişmiyor.
ÖRNEKTEKİ SONUÇ YANLIŞ 400 OLMALI
400 N doğru cevap, düzeltildi. Dikkatiniz için teşekkürler.
Ben Teşekkür ederim
Böcekler gibi küçük canlıların dayanıklılıkları neden yüksektir sorusuna yanlış bilgi yazmışsınz . Kesit alanlarının hacimlerine oranı DİĞER CANILARINKİNE ORANLA BÜYÜKTÜR yazmanız gerekirdi.
Dikkatiniz harika. Düzeltildi.
Bence dinozorlar yaşamış olabilirler çünkü üçgen yapılı bir cisim dikdörtgen yapılı bir cisimden daha dayanıklıdır ve dinozorların yapılarına bakıldığında vücutlarının alt kısmı üst kısımlarına göre çok geniştir.Ya da Eyfel Kulesi’nin mimarisi gibi kemik yapıları ağırlıklarını az tutup dayanıklılıklarını fazla yapacak şekilde olabilir.Evren aklımızın eremediği birçok olayla dolu, bazı durumlar bildiğimiz kuralların çok dışında, garipsediğimiz şekilde gerçekleşebiliyor.Neden olmasın!
Ben 50 yaşındayım. Ev hanımıyım. Oğlum bu konuyu anlamadığını söyleyince internette sizi buldum.
Biraz dikkatimi vererek okudum. Yazdıklarınızın hepsini anladım fakat ip sorusunun son satırındaki F
neydi anlayamadım. Okumaya devam…
Çok güzel anlatmışsınız hakkınızı helal edin. Benden küçük yada büyük olmanız farketmez yazan ellerini öpüyorum.
F kuvvet, yani ipin taşıyabileceği kuvvet miktarı.
Hocam başlarda yazdığınız
kesit alanı/ d•V•g. formülüne bakarak aynı kesit alanı ve hacme sahip iki cismin özkütlesi büyük olanın dayanıklılığı düşüktür diyebiliyor muyuz yani. Akılda canlandırınca biraz tuhaf geldi de?
Binanın alt kolonlarının kesit alanları arttıkça neden dayanıklılık da artar?Aslında formülde düşündüğümüzde hacim de taban alanını dahil ettiğinden 1/h olur böylece sabitlik gözlenmez mi?Yoksa sondaki ip sorusu gibi kuvvet bazında inceleyip dayanıklılığın binanın tüm kolonlarında kesit alanı/kuvvet’den sabit olduğunu mu söyleriz?Bir de bir düzine kağıttansa bir tane kağıdı yırtmak neden daha kolaydır bunu da merak ediyorum.Cevaplarsanız çok sevinirim,teşekkürler.
yani bu mantıkla kolonun kendi ağırlığına karşı dayanıklılığı ve dışarıdan uygulanan bir ağırlığa olan dayanıklılığını farklı sabitler belirlemiş oluyor diye mi düşünüyoruz?
Yeni ögrendim burayı çok iyi açıklanmış emeğinize saglık.
DAYANIKLILIKip = (π.2cm.2cm)/100N = 0,04π cm2/N
DAYANIKLILIKip = (π.4cm.4cm)/F
0,04π cm2/N = (16π cm2)/F
F = 400 N
–Sizin yazdığınıza göre 12,56 cm2/N değil 0,1256 cm2/N olması gerekiyor, aşağıda tekrar 100 ile çarpmak yanlış değil mi?
100 N ile çaptık sonucu. Ama daha anlaşılır olsun diye tekrar düzenledim çözümü.
Hocam selamlar çok güzel bir anlatım olmuş fakat ödevim için günlük hayattan daha çok dayanıklılık örneklerine ihtiyacım var rica etsem yardımcı olabilir misiniz ?
hocam bir cismin boyutları hangi oranda artarsa o oranda azalır . ifadesi doğru mu soruda gördüm çözümde geometrik cisimler için doğru kabul etmiş ama soruda o bilgiyi vermemiş ben yanlış demiştim o yüzden nasıl olmalı cevap.
Düzgün geometrik cisimler için cismin boyutları hangi oranda artarsa dayanıklılık o oranda azalır.