Özkütle ya da yoğunluk nedir? Tanımı ve grafikleri

Özkütle nedir sorusunun fizikte yanıtı bir cismin kütlesinin hacmine oranıdır. Bir maddenin birim hacmine ne kadar kütle sıkıştırılmış, yani yoğun olduğunun göstergesidir. Bu yüzden yoğunluk da denir. Matematiksel olarak özkütle ya da yoğunluk şöyle gösterilir (Özkütlenin veya yoğunluğun formülü):

d=\frac{m}{V}

m cismin kütlesini, V hacmini gösterir.

Özkütlenin birimi kg/m³‘tür, g/cm³ olarak da verilebilir. Kütle ve hacim skaler olduğu için özkütle de skalerdir, ayrıca türetilmiş bir büyüklüktür.

Yoğunluk sabit sıcaklık ve basınçta sabittir, ama sıcaklık ya da basınç değişirse o da değişir. Çünkü hacim, sıcaklık ve basınca göre değişir (oysa kütle değişmez). Özkütle maddenin ayırt edici bir özelliğidir, sabit sıcaklık ve basınçta tüm maddelerin özkütleleri birbirinden farklıdır.

Grafiklerden Özkütle Hesaplama

Bir öğrenci 5 cam bilye ile bir deney yapıyor. Odanın sıcaklığının ve basıncının sabit olduğunu kabul ediyor. Amacı cam için kütle ve hacim ilişkisini araştırmak. Bunun için cam bilyelerin kütlelerini ölçüyor, sonra birer birer su dolu dereceli silindirin içine atarak hacimlerini ölçüyor. Ölçüm sonuçları aşağıdaki tabloda verilmiş. Son sütunda kütlenin hacme oranını hesaplayıp yazmış.

Kaç bilye	Kütle – m (g)	Hacim – V (cm3)	m / V (g / cm3)
1	5	2	2,5
2	10	4	2,5
3	15	6	2,5
4	20	8	2,5
5	25	10	2,5

Bu verileri kullanarak üç grafik çizebiliriz:

Kütle hacim grafiğinden yoğunluk

Tablodaki verilerden eğer kütle ve hacim sayı çiftlerini kullanırsak bir grafik çizebiliriz. Bu grafik şöyle görünür.

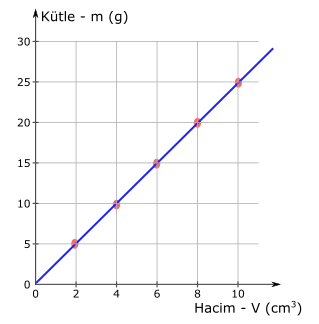
Kütlenin hacme bağlı olarak nasıl değiştiğini gösteren fonksiyon bir doğrudur (mavi çizgi). Bu doğrunun eğimi kütlenin hacme oranını yani özkütleyi verir. Kütle hacim grafiği bize kütle arttıkça hacmin de arttığını ve özkütlenin sabit kaldığını gösteriyor. Bu grafiğe göre özkütleyi, mavi doğrunun üstündeki herhangi bir noktayı kullanarak hesaplayabiliriz. Örneğin (m,V)=(15 g, 6 cm³) noktasını alalım:

d=\frac{m}{V} = \frac{15 \space g}{ 6 \space cm^3}= 2,5 \space g/cm^3

Özkütle hacim grafiği

Tablodaki verilerden son sütunda yer alan özkütle ile buna karşılık gelen hacim sayı çiftlerini kullanarak bir grafik daha çizebiliriz.

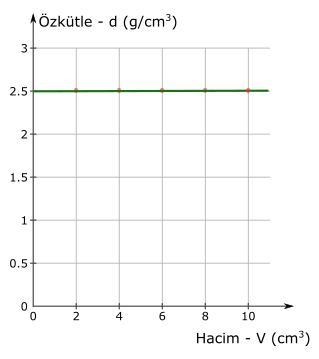
Özkütlenin hacme göre nasıl değiştiğini gösteren fonksiyon hacim eksenine paralel bir doğrudur (yeşil çizgi), eğimi sıfırdır. Hacim artsa da özkütle sabit kalıyor. Bu, özkütle hacme göre değişmez anlamına gelir. Hacim artmasına rağmen cam bilyelerin özkütlesi 2,5 g/cm³ kalmış.

Özkütle kütle grafiği

Tablodaki verilerden özkütle ile buna karşılık gelen kütle sayı çiftlerini kullanarak son bir grafik daha çizebiliriz.

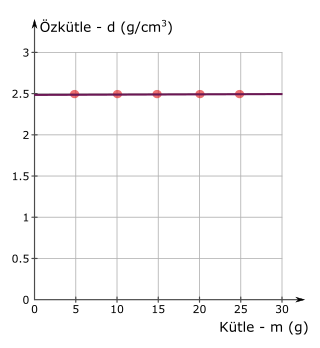
Özkütlenin kütleye göre değişimini gösteren fonksiyon kütle eksenine paralel bir doğrudur (mor çizgi), eğimi sıfırdır. Kütle artsa da özkütle değişmiyor. Bu, özkütle kütleye göre değişmez demektir. Kütle artsa da cam bilyelerin özkütlesi hep 2,5 g/cm³ olmuş.

Farklı maddelerin kütle hacim grafikleri ile özkütle karşılaştırması

Aşağıdaki tabloda farklı dört metalin eşit hacimleri için (V = 10 cm³) kütle ve özkütle değerleri verilmiş.

Madde türü	Kütle – m (g)	Hacim – V (cm3)	m/V (g / cm3)
Demir	78	10	7,8
Kurşun	113	10	11,3
Cıva	136	10	13,6
Altın	193	10	19,3

Bu değerlerin kütle hacim grafiğinde gösterimi şöyledir:

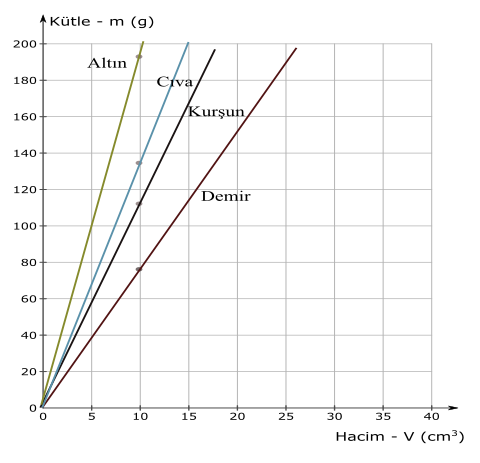
Özkütle arttıkça kütle hacim grafiğinin eğimi artar. Üstteki grafikte en dik eğimin altının, sonra cıvanın, sonra kurşunun, en son da demirin eğimi olduğu görülüyor.

Saf maddeler için özkütle hesaplanması

Saf maddeler tek bir element ya da bileşikten oluşur, yapılarında yabancı başka madde bulunmaz. Örneğin, saf su, altın, gümüş, cıva ya da kurşun saf maddedir. Saf maddelerde özkütle hesaplanırken tanımda verdiğimiz matematik modeli kullanılır.

Örnek soru 1 – Özkütle ve hacimden kütle hesaplama

Özkütlesi 2,7 g/cm³ olan saf alüminyumdan yapılmış hacmi 20 cm³ olan bir bloğun kütlesi kaç gramdır?

Çözüm:

Özkütlenin tanımını hatırlayalım.

d = \frac{m}{V}

Buradan kütleyi çekebiliriz. Eşitliğin iki tarafını da V ile çarpalım.

V \times d =\frac{m}{\cancel{V}} \times \cancel{V} m = d \times V

Artık sayıları yerleştirebiliriz.

m= 2,7 \space g/cm^3 \times 20 \space cm^3 = 54 \space g

Örnek soru 2 – Özkütle ve kütleden hacim hesaplama

Kütlesi 120 g, özkütlesi 0,8 g/cm³ olan saf etil alkolün hacmi kaç cm³‘tür?

Çözüm:

Yine tanımdan başlayalım:

d = \frac{m}{V}

Bu kez hacmi çekelim. Eşitliğin iki tarafını da önce V ile çarpalım, sonra d‘ye bölelim.

V \times \cancel{d} \times \frac{1}{\cancel{d}} = \frac{m}{\cancel {V}} \times \cancel{V} \times \frac{1}{d} V=\frac{m}{d}

Şimdi sayıları yerleştirebiliriz.

V=\frac{120 \space g}{0,8 \space g/cm^3} = 150 \space cm^3

Karışımlar ve alaşımlar için özkütle hesaplanması

İki ya da daha fazla saf maddenin bir araya gelmesiyle oluşan maddelere karışım denir. Şekerli su, tuzlu su ve hava karışımdır. Biri metal olmak üzere iki ya da daha fazla maddenin bir araya gelmesinden oluşan maddelere alaşım denir. Örneğin tunç, bakır ve kalay metallerinin oluşturduğu bir alaşımdır. Aşağıdaki örnek soru sadece Fen Lisesi öğrencileri için, bunu isterseniz geçebilirsiniz.

Örnek soru 3 – Etil alkol ve su karışımının özkütlesi

Özkütleleri sırasıyla 0,8 g/cm³ ve 1 g/cm³ olan etil alkol ve saf su karıştırılarak homojen bir karışım elde ediliyor. Kullanılan etil alkolün hacmi 50 cm³, saf suyunki 70 cm³ ise, karışımın özkütlesi kaç g/cm³ olur?

Çözüm:

Tanım tanım tanım. Hepsi tanımdan çözülür. Son kütleyi son hacme bölünce karışımın özkütlesi bulunur. Kütleleri hesaplayıp toplayacağız, sonra hacimleri hesaplayıp toplayacağız. Toplam kütlenin toplam hacme oranı özkütleyi verecek.

d_{karisim}=\frac{m_{toplam}}{V_{toplam}} m_{toplam} = m_{etil \space alkol} + m_{su} m_{etil \space alkol} = d_{etil \space alkol} \times V_{etil \space alkol} m_{etil \space alkol} = 0,8 \space g/cm^3 \times 50 \space cm^3 = 40 \space g m_{su} = d_{su} \times V_{su} m_{su} = 1 \space g/cm^3 \times 70 \space cm^3 = 70 \space g m_{toplam} = 40 \space g + 70 \space g = 110 \space g V_{toplam} = V_{etil \space alkol} + V_{su} V_{toplam} = 50 \space cm^3 + 70 \space cm^3 = 120 \space cm^3 d_{karisim}=\frac{110 \space g}{120 \space cm^3} = 0,92 \space g/cm^3

Bu sorunun sonucu önemli. Bize karışımın özkütlesinin karışımı oluşturan maddelerin özkütleleri arasında olduğunu gösteriyor. d_su > d_karışım > d_{etil alkol}. Aşağıdaki grafik bu sonucun özeti.

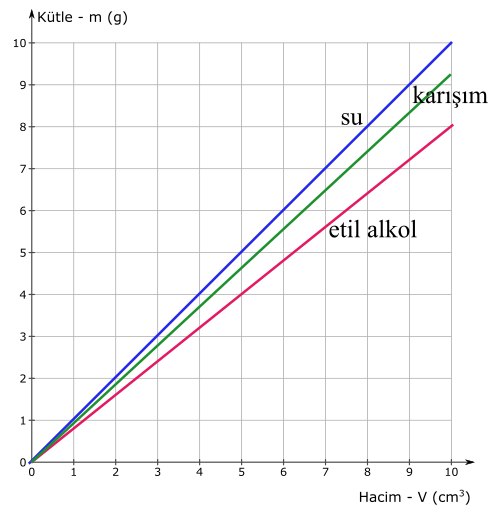
Eşit hacimli ya da eşit kütleli iki maddenin homojen karışımının özkütle formüllerini çıkarabilirsiniz, ama kesinlikle ezberlemeyin. Hangisi hangisiydi unutursunuz, tanımdan çözmek her zaman daha kolaydır ve garantilidir.

Günlük hayatta özkütle

• Kuyumcular altının kaç ayar olduğunu belirlemek için getirilen takıların özkütlesini hesaplar. Örneğin, 22 ayar altın bir alaşımdır, %91,6 saf altın içerir, gerisi bakır gibi başka metallerden oluşur.
• Porselen yapımında, farklı sertlik ve dayanıklılıkta malzeme üretmek için hangi maddeden ne kadar koymak gerektiği özkütleler hesaplanarak belirlenir.

Özkütle Problemleri

1. Yarıçapı 10 cm olan küre şeklindeki bir bakır topun kütlesi ne kadardır? (d_bakır = 8,96 g/cm³)
2. Bir ayrıtı 20 cm olan küp şeklinde bir tahta bloğun kütlesi 5,6 kg olduğuna göre, özkütlesi kaç g/cm³‘tür?

Özkütle ile ilgili Fizik dersi Kazanımları

9.2.1.1. Özkütleyi, kütle ve hacimle ilişkilendirerek açıklar.

• Sabit sıcaklık ve basınçta ölçüm yapılarak kütle-hacim grafiğinin çizilmesi; kütle, hacim ve özkütle kavramları arasındaki matematiksel modelin çıkarılması sağlanır.
• Kütle-özkütle, hacim-özkütle grafiklerinin çizilmesi ve yorumlanması sağlanır.
• Karışımların özkütlelerine değinilir. Matematiksel hesaplamalara girilmez.
• Archimedes ve el-Hazini’nin özkütle ile ilgili yaptığı çalışmalara kısaca değinilir.

9.2.1.2. Günlük hayatta saf maddelerin ve karışımların özkütlelerinden faydalanılan durumlara örnekler verir.

• Kuyumculuk, porselen yapımı, ebru yapımı gibi özkütleden faydalanılan çalışma alanlarına değinilir.