Esnek çarpışmalar nedir? Örnek soru çözümleri

Momentumun korunumu kanunun uygulamalarından en önemlilerinden biri çarpışmalardır. Çarpışmaların özel bir durumu olan esnek çarpışmalarda çarpışan cisimlerin hem çizgisel momentumu hem de kinetik enerjisi korunur. Yani kapalı bir sistemin çarpışmadan önceki ve sonraki kinetik enerjileri birbirine eşitse, bu tür çarpışmalar esnek çarpışma olarak adlandırılır. Sistemin kinetik enerjisinin korunmadığı durumlara is esnek olmayan çarpışma denir, bunu bir sonraki yazıda anlatacağız. Esnek çarpışmaları bir boyutta ve iki boyutta inceleyeceğiz.

Bir boyutta esnek çarpışmalar

Bir boyutta esnek çarpışmalara merkezi çarpışma da denir. Çünkü çarpışma sırasında cisimlerin merkezleri aynı doğrultudadır. Aşağıdaki animasyona bir bakalım.

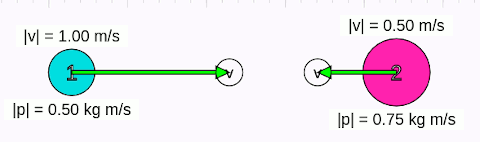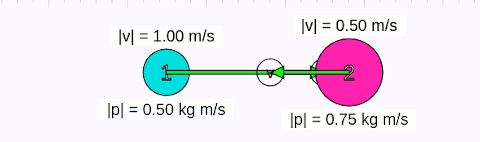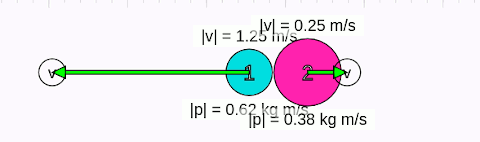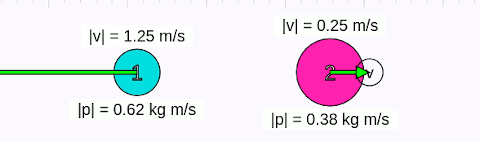
Animasyonda başlangıçta 1 numaralı cismin hızının sağa doğru (+x yönünde) 1 m/s, 2 numaralı cismin hızının sola doğru (-x yönünde) 0,5 m/s olduğunu görüyoruz. Birinci cismin kütlesi 0,5 kg, ikincinin ki 1,5 kg, başlangıç momentumları eşit değil. Çarpışmadan sonra her iki cismin de momentumlarının büyüklüğünün değiştiğini görüyoruz. Çarpışmanın ardından, birinci cisim -x yönünde doğru 1,25 m/s, ikinci cisim +x yönüne doğru 0,25 m/s hızla hareket ediyor. Şimdi matematiksel olarak bu durumu anlamaya çalışalım.

Sistemin ilk momentumu, son momentumuna eşit olmak zorunda:
\vec{p_1} + \vec{p_2} = \vec{p'_1} + \vec{p'_2}

m_1\vec{v_1} + m_2\vec{v_2} = m_1\vec{v'_1} + m_2\vec{v'_2}

Düzenlersek:
m_1(\vec{v_1} - \vec{v'_1}) = m_2(\vec{v_2} - \vec{v'_2})
Şimdi kinetik enerjinin korunumunu yazalım.
E_{K1} + E_{K2} = E'_{K1} + E'_{K2}

\frac{1}{2} m_1 v_1^2 + \frac{1}{2} m_2 v_2^2 = \frac{1}{2} m_1 v_{1}^{'2} + \frac{1}{2} m_2 v_{2}^{'2} \frac{1}{2} m_1 v_1^2 - \frac{1}{2} m_1 v_{1}^{'2} = \frac{1}{2} m_2 v_{2}^{'2} - \frac{1}{2} m_2 v_2^2 m_1(v_1^2 - v_{1}^{'2} ) = m_2(v_{2}^{'2} - v_2^2) m_1(v_1 - v_1')(v_1+v_1') = m_2(v_2' - v_2)(v_2'+v_2)

Bu vektörel çarpıma eşit:
m_1(\vec{v_1} - \vec{v_1'}) . (\vec{v_1}+\vec{v_1'}) = m_2(\vec{v_2'} - \vec{v_2}).(\vec{v_2'}+\vec{v_2})
Şimdi kinetik enerji ve momentum korunumlarını oranlayabiliriz:
\frac{m_1(\vec{v_1} - \vec{v_1'}) . (\vec{v_1}+\vec{v_1'})}{m_1(\vec{v_1} - \vec{v'_1})} = \frac{m_2(\vec{v_2'} - \vec{v_2}).(\vec{v_2'}+\vec{v_2})}{m_2(\vec{v_2} - \vec{v'_2})}
Şimdi ilginç sonuç geliyor. Yukarıdaki eşitliği düzenlersek:
\vec{v_1}+\vec{v_1'} =\vec{v_2'}+\vec{v_2}
Merkezi esnek çarpışma yapan cisimlerden birinin çarpışmadan önceki ve sonraki hızlarının toplamı, diğerinin çarpışmadan önceki ve sonraki hızlarının toplamına eşit. Animasyondan kontrol edelim. Birinci cismin ilk hızı +x yönünde 1 m/s, son hızı -x yönünde 1,25 m/s. İkinci cismin ilk hızı -x yönünde 0,5 m/s, son hızı +x yönünde 0,25 m/s. Bakalım tutuyor mu:
1 + (-1,25) = - 0,5+0,25

-0,25 = -0,25

Tutuyor. Matematik yalan söylemez, ama işlem hatası yapabiliriz.

Bir başka ilginç sonuç daha var. Bağıl hız cinsinden yazalım yukarıdaki eşitliği:

\vec{v_1} -\vec{v_2} = -(\vec{v_1'} - \vec{v_2'})

Merkezi esnek çarpışmalarda iki cismin çarpışmadan önceki bağıl hızları, çarpışmadan sonraki bağıl hızlarının eksi işaretlisine eşit oluyor.

Eşit momentumlu cisimler için merkezi çarpışmalar

Önce aşağıdaki animasyonu inceleyelim sonra daha genel çıkarımlar yapalım. Cisimlerin merkezleri doğrultusunda çarpıştıklarına dikkat edin.

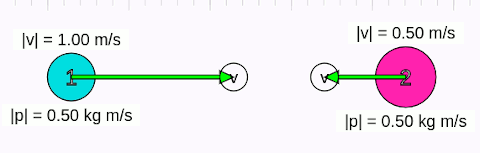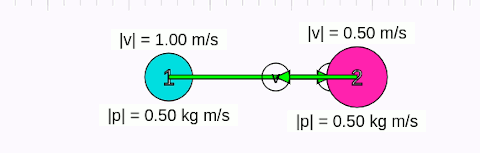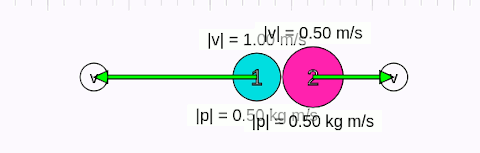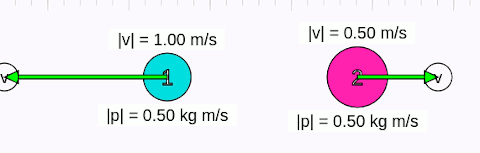
Yukarıdaki animasyonda başlangıçta 1 numaralı cismin hızının sağa doğru (+x yönünde) 1 m/s, 2 numaralı cismin hızının sola doğru (-x yönünde) 0,5 m/s olduğunu görüyoruz. Birinci cismin kütlesi 0,5 kg, ikincinin ki 1 kg. Başlangıç momentumlarının büyüklüğü her iki cisim için de 0,5 kgm/s. Çarpıştıktan sonra her iki cismin momentumunun büyüklüğünün aynı olduğunu, ama momentum vektörlerinin yönünün değiştiğini görüyoruz. Çünkü, cisimlerin hız vektörlerinin yönü değişiyor. Ama cisimlerin hızlarının büyüklüğünün (yani süratlerinin) değişmediğine dikkat edin. Yani merkezi çarpışmada, çarğışmadan sonra cisimler geldikleri süratle aynı fakat zıt yönde hareket ediyorlar.

Örnek soru 1

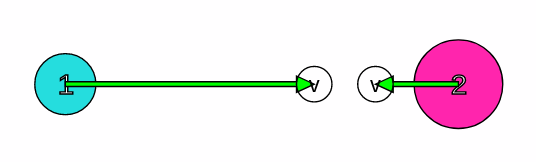
Şekildeki 1 kg kütleli 1 numaralı) mavi cisim 12 m/s, 3 kg kütleli (2 numaralı) pembe cisim 4 m/s büyüklüğündeki hızlarla birbirlerine doğru gelip, merkezi esnek çarpışma yapmaktadır. Buna göre cisimlerin çarpışmadan sonraki hızlarının büyüklükleri kaç m/s olur?

Çözüm

Önce momentumun korunumunu yazalım:
m_1\vec{v_1} + m_2\vec{v_2} = m_1\vec{v'_1} + m_2\vec{v'_2}
Sonra bildiğimiz değerleri yerleştirelim:
12 - (3)4 = (1)\vec{v_1'} + (3)\vec{v_2'}

\vec{v_1'} + 3\vec{v_2'} = 0

Yani:

\vec{v_1'} = - 3\vec{v_2'}

Ayrıca merkezi çarpışmalar için şu sonuca varmıştık:

\vec{v_1}+\vec{v_1'} =\vec{v_2'}+\vec{v_2}

Değerleri yerleştirelim:
12 + \vec{v_1'} = -4 + \vec{v_2'}
Düzenleyelim:
\vec{v_1'} - \vec{v_2'} = 4 - 12 = -16

Az önce bulduğumuz ilk denklemden v’₁ yerine koyalım.
-3\vec{v_2'} - \vec{v_2'} = -16

-4\vec{v_2'} = -16 \vec{v_2'} = 4 m/s

Şimdi de ilk cismin son hızını bulalım:
\vec{v_1'} = - 3(4m/s)= -12 m/s

Eşit çizgisel momentumlarla merkezi esnek çarpışma yapan cisimlerin çarpışmadan sonra kendi hızlarının büyüklüğünde hızlarla geri döndüklerini görmüş olduk.

Eşit kütleli cisimler için merkezi çarpışmalar

Bir de kütlelerin eşit olduğu durumu inceleyelim. Yine bir animasyonumuz var.

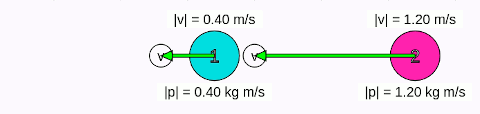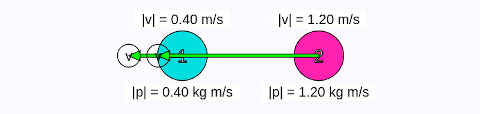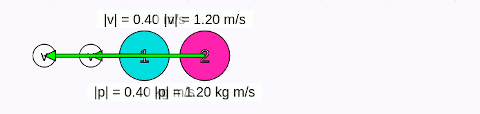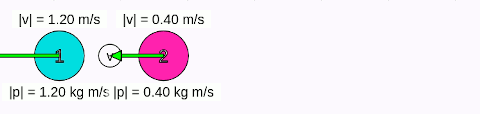
Yukarıdaki animasyona dikkat ederseniz bu kez karşılıklı değil kütleler. Çarpışmalar mutlaka karşılıklı kafa kafaya olmak zorunda değil. Ama 2 numaralı cismin hızı 1 numaralıdan büyük olduğu için yeişip arkadan çarpıyor. Çarpışmadan önce 1 numaralı cismin hızı -x yönünde 0,4 m/s ve 2 numaralı cisminki yine -x yönünde 1,2 m/s. Çarpışmadan sonra cisimler birbirlerinin süratlerini alıyorlar. Bu ilginç bir sonuç, ayrıca cisimlerin hızları da aynı yani hızın yönü de aktarılıyor.

Örnek soru 2

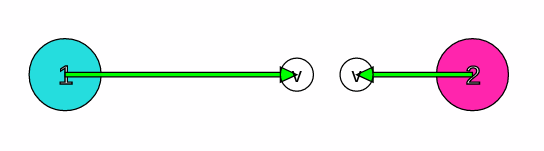
Şekilde gösterilen ikisi de 3 kg kütleli 1 ve 2 numaralı cisimler sırasıyla 12 m/s ve 4 m/s hızlarla bir boyutta esnek çarpışma yapmaktadır. Buna göre cisimlerin çarpışmadan sonraki hızları kaç m/s olur?

Çözüm

Yine momentumun korunumunu yazalım.

m_1\vec{v_1} + m_2\vec{v_2} = m_1\vec{v'_1} + m_2\vec{v'_2}

Değerleri yerleştirelim.
3(12) + 3(-4) = 3(\vec{v'_1} + \vec{v'_2})
Düzenleyelim.
3(12-4) = 3(\vec{v'_1} + \vec{v'_2})

\vec{v'_1} + \vec{v'_2} = 8 \vec{v'_1} = 8 - \vec{v'_2}

Şimdi de merkezi çarpışmalar için vardığımız sonucu yazalım:
\vec{v_1}+\vec{v_1'} =\vec{v_2'}+\vec{v_2}
Bunu da düzenleyelim.
\vec{v_1'} - \vec{v_2'} = \vec{v_2} - \vec{v_1}
Değerleri yerine yazalım.
\vec{v_1'} - \vec{v_2'} = -4 - (12) = -16

Artık ilk denklemde yerine yerleştirelim.
8 - \vec{v'_2} - \vec{v'_2} = -16

-2 \vec{v'_2} = -16 - 8 = -24 \vec{v'_2} = 12m/s

İkinci cismin çarpışmadan sonraki hızının büyüklüğünün ilk cismin çarpışmadan önceki hızının büyüklüğüne eşit olduğunu bulduk. Ayrıca yönleri de aynı bu hızların. Yani hızın sadece büyüklüğü değil yönü de aktarılıyor. Şimdi bir de ilk cismin son hızına bakalım.
\vec{v'_1} = 8 - (12) = -4 m/s
Yine aynı sonuç. Birinci cisimin çarpışmadan sonraki hızı (hem büyüklüğü hem yönü) ikinci cismin çarpışmadan önceki hızına eşit çıktı.

İki boyutta esnek çarpışmalar

Esnek çarpışmalarda çizgisel momentumun ve kinetik enerjinin korunduğunu söylemiştik, bu hem bir boyutta hem iki boyutta çarpışmalar için geçerli. İki boyutlu çarpışmalarda çarpışma cisimlerin merkezlerini birleştiren doğru üzerinde olmaz. Bu nedenle cisimler çarpışmadan önce ve sonra tek doğrultuda ilerlemez. İşte bu yüzden cisimlerin çizgisel momentumu iki boyutta incelenir. Ayrıntılı olarak bakalım.

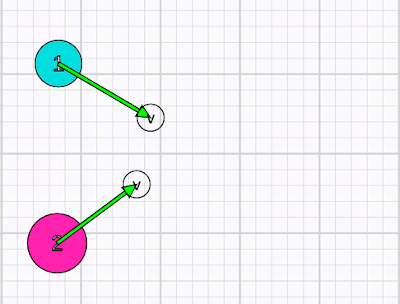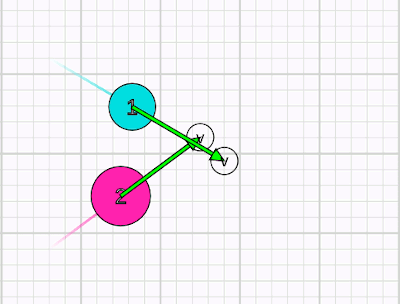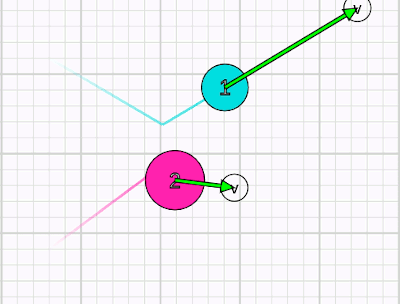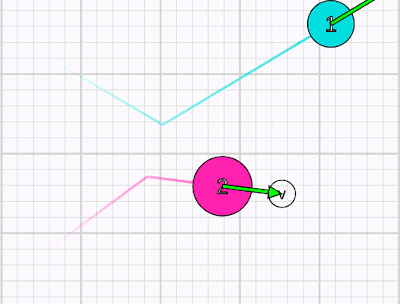
Yukarıdaki animasyonda iki cismin esnek çarpıştığını ama merkezi çarpışmadığını görüyoruz. Çizgisel momentum hala korunuyor. Bunu geometrik olarak inceleyelim. Önce çarpışmadan önceki duruma bakalım.

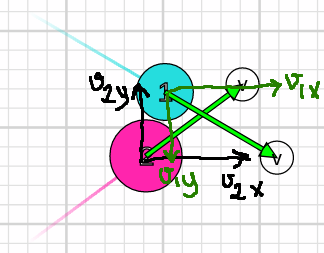
Her iki cismin de ilk hızlarını dolayısıyla momentumlarını x ve y eksenlerinde bileşenlerine ayırıyoruz. Toplam başlangıç momentumumuz bu olacak.

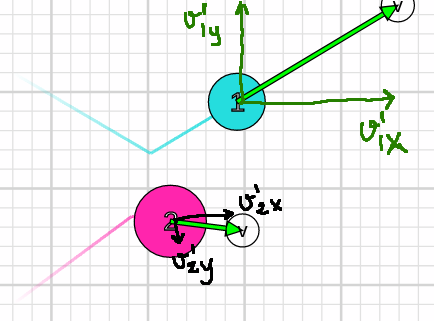
Aynı şeyi, yani x ve y bileşenlerine ayırma işlemini çarpışmadan sonraki momentum ve hız bileşenleri için de yapacağız. Momentumun vektörel olarak korunması demek, momentumun x bileşenlerinin ve y bileşenlerinin, başlangıçta ve sonda birbirine eşit olması demek.
p_{1x} + p_{2x} = p'_{1x} + p'_{2x}
Dolayısıyla:

m_1 v_{1x} + m_2 v_{2x} = m_1 v'_{1x} + m_2 v'_{2x}

p_{1y} + p_{2y} = p'_{1y} + p'_{2y}
Benzer şekilde:

m_1 v_{1y} + m_2 v_{2y} = m_1 v'_{1y} + m_2 v'_{2y}

Ayrıca kinetik enerji de korunuyor.
\frac{1}{2}m_1(v_{1x}^2 + v_{1y}^2) + \frac{1}{2}m_2(v_{2x}^2 + v_{2y}^2) = \frac{1}{2}m_1(v_{1x}^{'2} + v_{1y}^{'2}) + \frac{1}{2}m_2(v_{2x}^{'2} + v_{2y}^{'2})

Örnek soru 3

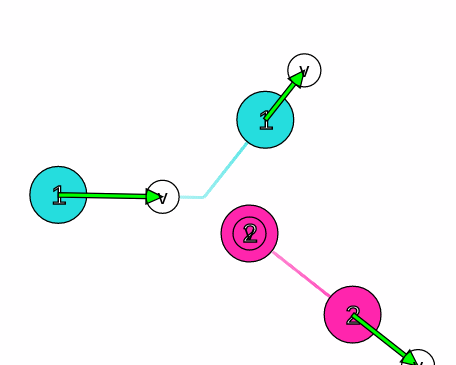
Şekilde gösterilen eşit kütleli iki cisimden 1 numaralı olanın hızının büyüklüpü v₁ dir, 2 numaralı cisim durmaktadır. Bu cisimler esnek çarpışma yaptıktan sonra hareket doğrultuları arasındaki açı kaç derece olur?

Çözüm

Cisimler esnek çarpışma yaptığı için çizgisel momentum ve kinetik enerji korunur. Momentumun korunumunu bu kez vektörel göstermeliyiz.

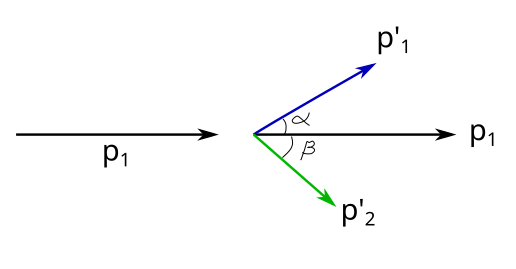
Buradan birinci cismin ilk hızına v₁, son hızına v’₁, ikinci cismin son hızına v’₂ diyebiliriz. Şimdi de enerjinin korunumunu yazalım.
\frac{1}{2}mv_1^2 + 0 = \frac{1}{2}m v_1^{'2} + \frac{1}{2}m v_2^{'2}

v_1^2 = v_1^{'2} + v_2^{'2}

Bu durum ancak bir dik üçgende mümkün, Pisagor bağıntısı bu. Öyleyse iki cismin hız vektörleri arasındaki açı 90 derece olmak zorunda.

Esnek çarpışmalar ile ilgili kazanımlar

11.1.7.4. Çizgisel momentumun korunumu ile ilgili hesaplamalar yapar.

• Enerjinin korunduğu ve korunmadığı durumlar göz önüne alınarak bir ve iki boyutta çizgisel momentumun korunumu, çarpışmalar ve patlamalarla ilgili matematiksel hesaplamalar yapılması sağlanır.