Patlamalar ve Kenetlenmeler: Örnek soru çözümleri

Momentumun korunumu ilkesini incelerken bir tane iç patlama sorusu çözmüştük. Bu yazıda iç patlamalara bir kaç örnek soruyla devam edeceğiz. Esnek olmayan çarpışmaları incelerken bir kaç tane kenetlenme sorusu da çözmüştük. Bir kaç soru daha çözeceğiz. Çizgisel momentumun korunumunun patlamalarda ve kenetlenmelerde nasıl kullanıldığını ayrıntılı olarak inceleyeceğiz.

Örnek soru 1 – yukarı yönlü atışta iç patlama

Kütlesi 9 kg olan bir cisim, aşağıdan yukarıya düşey olarak 30 m/s ilk hızla atılıyor. Cisim 2 saniye sonra 3 kg ve 6 kg kütleli iki parçaya ayrılıyor. 3 kg kütleli parça patlamadan sonra serbest düşme hareketi yapıyor. Buna göre 6 kg kütleli parça yerden en fazla kaç metre yüksekliğe kadar çıkabilir? (g = 10m/s², hava direncini ihmal ediniz.)

Çözüm

Soru korkutucu mu göründü. Böl ve fethet yöntemini kullalım. Önce soruyu görselleştirmemiz lazım. Görmeden tam anlayamayız. Çizelim.

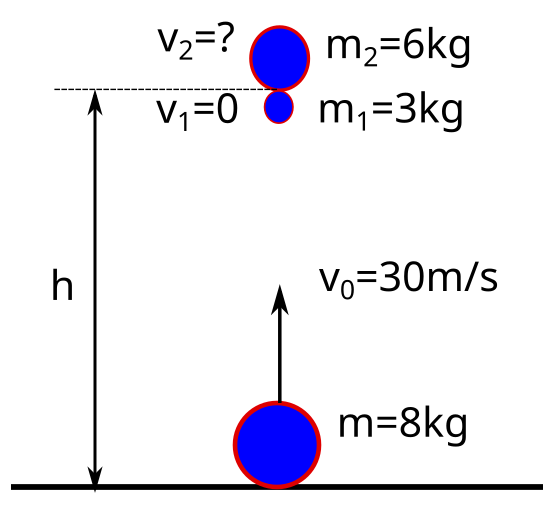
Çizimimizi okumamız lazım. Cisim aşağıdan yukarıya doğru atış hareketi yapıyor. Atıldıktan 2 saniye sonra patlıyor. Öyleyse cismin patlamadan hemen önceki hızını bulabiliriz.
v = v_0 - gt

v = 30 - 10(2) = 30 -20 = 10 m/s

Bütün halindeyken cismin patlamadan hemen önceki hızı yukarı yönlü 10 m/s. Bu önemli çünkü momentumun korunumu prensibi patlamadan sonra parçaların hızını bulmaya yarayacak.
\vec{p} = \vec{p_1} + \vec{p_2}

Birinci parçanın patlamadan hemen sonra serbest düşme yaptığını biliyoruz. Bunun anlamı ilk hızının olmaması yani sıfır olması demek. Öyleyse birinci parçanın momentumu da sıfır olmak zorunda. Bu durumda ikinci parçanın momentumu cismin patlamadan hemen önceki momentumuna eşit olmak zorunda, ayrıca vektörel olarak da eşitlik söz konusu. Yani hızlarının yönleri de aynı olmalı.
\vec{p} = 0 +\vec{p_2}

m\vec{v} = m_2\vec{v_2} (9)10 = 6v_2 \vec{v_2} = 15 m/s

Artık patlamadan hemen sonra ikinci parçanın yukarı yönlü 15 m/s ile hareket ettiğini biliyoruz. Hızları bildiğimize göre yükseklikleri hesaplayabiliriz. Önce patlamadan hemen önceki yüksekliği hesaplayalım.
h = v_0t - \frac{1}{2}gt^2

h = 30(2) - \frac{1}{2}(10)(2^2) h = 60 - 20 = 40 m

Şimdi patlamadan sonra ikinci parçanın maksimum yüksekliğini hesaplayalım. Zamansız hız formülüyle işimiz daha kolay.
v_2^2 = 2gh_2

h_2 = \frac{v_2^2}{2g} h_2 = \frac{15^2}{2(10)} = \frac{225}{20} = 11,25 m

Şimdi toplam yüksekliği, yani ikinci parçanın yerden en yüksek olabileceği yüksekliği bulabiliriz.
h_t = h + h_2 = 40 + 11,25 = 51,25 m

Yüksekliği çözmenin bir yolu da enerjinin korunumundan gitmek, onu da gösterelim. İkinci cismin patlamadan sonraki kinetik enerjisi, en yüksek noktadaki potansiyel enerjisine eşit olmalı. Zamansız hız formülünün nereden geldiğini gösterip bırakalım.
E_k = E_p

\frac{1}{2}m_2v_2^2 = m_2gh_2

Düzenlersek:
v_2^2 = 2gh_2

Örnek soru 2 – eğik atışta iç patlama

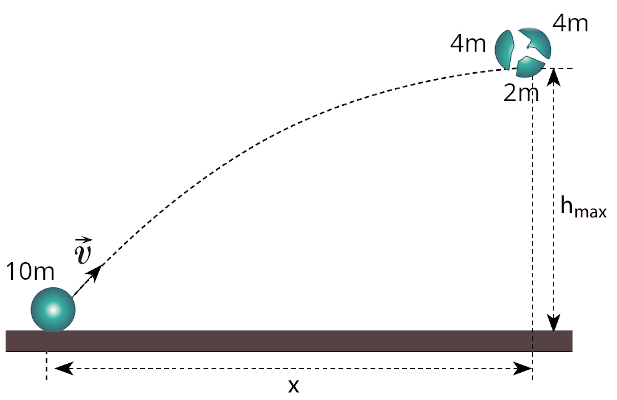
Hava direncinin ihmal edildiği ortamda yerden eğik olarak V hızıyla atılan 10m kütleli cisim çıkabileceği en yüksek yükseklikte iç patlamayla üç parçaya ayrılıyor. Bu noktaya gelene kadar yatayda x kadar yol alıyor. Patlamadan hemen sonra 2m kütleli serbest düşme hareketi yapıyor. 4m kütleli parçalardan biri cismin atıldığı ilk noktaya düşüyor. Buna göre diğer 4m kütleli parça cismin atıldığı noktadan kaç x uzağa düşer?

Çözüm

Bu soru da korkutucu görünmüş olabilir. Yine parçalayıp çözeceğiz. Bu bir eğik atış sorusu. Öyleyse, eğik atışla ilgili bildiklerimizi hatırlayalım. Cismin çıkabileceği maksimum yüksekliğe tepe noktası diyorduk. Tepe noktasında sadece yatay hız vardı, düşey hız sıfırdı. Ayrıca eğik atışta yatay hız hiç değişmiyordu. Eğik atışın başlangıcındaki v hızının yatayla (x – ekseniyle) yaptığı açı cinsinden yatay hızı bulabiliriz:
v_x = vcos \theta

Tepe noktasındaki hız bu yatay hız.

Başka ne biliyoruz. Soru bize 4m kütleli parçalardan birinin geri tepip cismin ilk bulunduğu noktaya düştüğünü söylüyor. Bu durum yalnızca bu parçanın hızı tam olarak cismin hızının zıt yönlüsüne eşit olursa mümkün. Bu parçaya A parçası diyelim.
\vec{v_A} = -\vec{v}cos \theta

2 m kütleli cisme de B parçası diyelim. B parçasının serbest düşme yaptığını biliyoruz. Demek ki hızı sıfır.
\vec{v_B} = 0

Artık momentumun korunumu ilkesini yazarak üçüncü parçanın hızını bulabiliriz. Üçüncü parçaya da C diyelim.
\vec{p} = \vec{p_A} + \vec{p_B} + \vec{p_C}

(10m)vcos \theta = -(4m)vcos \theta + 0 + (4m)\vec{v} 4m\vec{v} = 14mvcos \theta \vec{v} = 3,5vcos\theta

C parçasının hızını bulduk. Artık aldığı yolu da bulabiliriz. Ama önce x ile v_x yani vcosθ arasındaki ilişkiyi çözelim. Yatayda hız değişmediğine göre, t sürede vcosθ hızıyla herhangi bir cisim x mesafesini katediyor.
x = (t)vcos\theta

Öyleyse 3,5vcosθ yatay hızı olan bir cisim 7x yol alır:
(t)3,5vcosθ = 3,5x

Cismin atıldığı noktadan uzaklığı da x + 3,5x = 4,5x olur.

Örnek soru 3 – kenetlenme balistik sarkaç

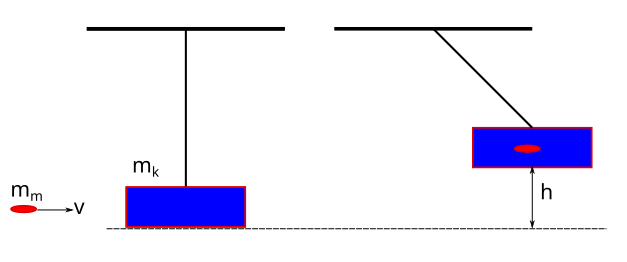
Mermilerin özelliklerini bulmakta kullanılan bir araç olan balistik sarkaçın bir modeli şekilde gösterilmiştir. Kütlesi 20 g olan bir mermi, ipin ucuna bağlı olarak duran 1980 g kütleli takoza 400 m/s hızla çarpıp saplanıyor. Buna göre:

(a) Çarpışma sonrası mermi ve takozun birlikte çıkabilecekleri maksimum yükseklik kaç metredir?

(b) Çarpışma sırasında sistemde diğer enerji türlerine dönüşen enerji miktarı kac Joule’dür? (g = 10 m/s², hava direncini ve çarpışma esnasında eksilen kütleyi ihmal ediniz.)

Çözüm

Bu soru da sandığınız kadar zor değil. Yine momentumun korunumunu kullanacağız. Çarpışmadan önceki ve sonraki momentumlar birbirine eşit olmak zorunda. Başlangıçta merminin hızı var, takozun hızı sıfır, dolayısıyla momentumu da sıfır.
\vec{p_{ilk}} = \vec{p_{son}}

m_m v_m + 0 = (m_m+m_k)v_{ortak}

Şimdi değerleri yerleştirelim.
(20 \times10^{-3} kg)(400m/s) = (20 \times10^{-3} + 1980 \times10^{-3} )v_{ortak}

Düzenleyelim:
(2000 \times 10^{-3}kg)v_{ortak} = 8 m/s

v_{ortak} = \frac{8}{2} = 4m/s

Bu bir esnek olmayan çarpışma olduğu için, çarpışma esnasında mekanik enerji korunmaz. Ama çarpışmadan sonra hava sürtünmesi ihmal edildiği için mekanik enerji korunur. Bu sorunun kilit noktası işte bu. Çarpışmadan hemen sonraki kinetik enerji, cisimler maksimum yüksekliğe çıktığında potansiyel enerjiye dönüşür. Öyleyse:
\frac{1}{2}(m_m + m_k)v^2 = (m_m +m_k)gh

v^2 = 2gh h = \frac{v^2}{2g} h = \frac{4^2}{2(10)} = \frac{16}{20} = 0,8 m

(b) Şimdi başlangıç ve son enerjilerin farkını bularak, sistemde diğer enerji türlerine dönüşen enerji miktarını hesaplayalım.
\Delta E = E_{ilk} - E_{son}

\Delta E = \frac{1}{2}m_mv_m^2 - (m_m + m_k)gh \Delta E = \frac{1}{2}(20 \times 10^{-3})(400^2) - (20 \times 10^{-3} + 1980 \times 10^{-3})(10)(0,8) \Delta E = 1600 - 16 = 1584 J

Çarpışma sırasında enerjinin büyük bir kısmı ısıya ve sese dönüşmüş.

Patlamalar ve Kenetlenmeler ile ilgili kazanımlar

11.1.7.4. Çizgisel momentumun korunumu ile ilgili hesaplamalar yapar.

• Enerjinin korunduğu ve korunmadığı durumlar göz önüne alınarak bir ve iki boyutta çizgisel momentumun korunumu, çarpışmalar ve patlamalarla ilgili matematiksel hesaplamalar yapılması sağlanır.