Esnek olmayan çarpışmalar nedir? Örnekler

Bir önceki yazımızda esnek çarpışmaları incelemiştik, şimdi sırada esnek olmayan çarpışmalar var. Bu tür çarpışmaların esnek çarpışmalarla ortak yanı çizgisel momentumun korunuyor olması. Farklı yanı ise kinetik enerjinin korunmaması. Bir başka deyişle esnek olmayan çarpışma demek momentumun korunduğu ama kinetik enerjinin korunmadığı çarpışma demektir. Sistemin çarpışmadan önceki kinetik enerjisi toplamı çarpışmadan sonrakinden büyüktür.

E₁ + E₂ > E’₁ + E’₂

Çarpışmadan sonra cisimler kenetlenerek birlikte hareket edebilir ya da ayrı ayrı hareket edebilirler. Çarpışma esnasında kinetik enerjinin bir kısmı ısıya ve ses enerjisine dönüşür.

Bir boyutta esnek olmayan çarpışmalar

Bir boyutta gerçekleşen esnek olmayan çarpışmalara merkezi esnek olmayan çarpışmalar da denir. Bunu bir örnekle daha iyi anlayabiliriz.

Örnek soru 1

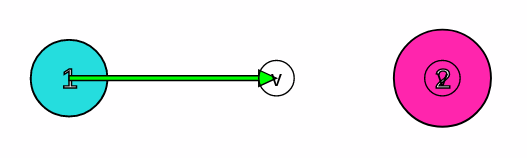
Sürtünmelerin ihmal edildiği yatay düzlemde m kütleli 1 numaralı (mavi) cisim 10v büyüklüğünde hız ile durmakta olan 2m kütleli (2 numaralı pembe) cisme merkezi çarpmaktadır. (a) Çarpışmadan sonra m kütleli cisim 2v süratle geri döndüğüne göre 2m kütleli cismin sürati kaç v olur? (b) Cisimler ne tür çarpışma yapmıştır?

Çözüm

Çizgisel momentumun korunumunu yazalım. Başlangıç momentumu (büyüklüğü ve yönü) son momentuma eşit olmak zorunda.
\vec{p_1} + \vec{p_2} = \vec{p'_1} + \vec{p'_2}

m\vec{v_1} + m\vec{v_2} = m\vec{v'_1} + m\vec{v'_2}

Değerleri yerleştirelim:
m(10\vec{v}) + 2m(0) = m(-2\vec{v}) + 2m\vec{v'_2}

10m\vec{v}+2m\vec{v} = 2m\vec{v'_2} \vec{v'_2} = 6\vec{v}

Kinetik enerji korunduysa esnek, korunmadıysa esnek olmayan çarpışma yapmışlardır. Bakalım kinetik enerji korunmuş mu.
\frac{1}{2}m(10v)^2 + 0 \stackrel{?}{=} \frac{1}{2}m(-2v)^2 + \frac{1}{2}2m(6v)^2

100mv^2 \stackrel{?}{=} 4mv^2 + 72mv^2 100mv^2 \neq 76mv^2

Kinetik enerji korunmamış, dolayısıyla bu esnek olmayan merkezi çarpışma. Ayrıca cisimlerin birbirine kenetlenmediğini yani yapışmadığını da görüyoruz.

Bir boyutta tamamen esnek olmayan çarpışmalar

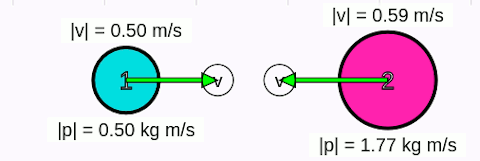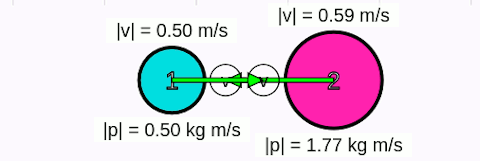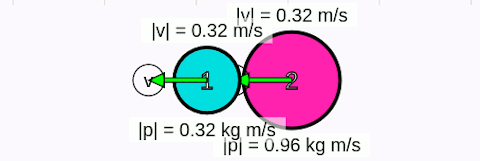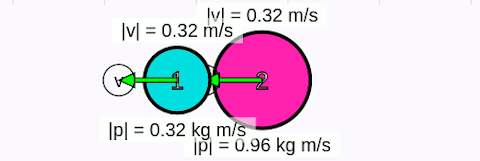
Tamamen esnek olmayan çarpışmalarda cisimler çarpışınca birbirine kenetlenir ya da yapışır. Çarpışmadan sonra cisimler ortak bir hızla hareket eder. Sistemin çarpışmadan önceki toplam çizgisel momentumu, çarpışmadan sonraki toplam çizgisel momentumuna eşit olur. Aşağıdaki animasyonda tamamen esnek olmayan merkezi çarpışma gösteriliyor. Cisimler kenetlenince hızlarının eşit olduğuna dikkat edin.

Örnek soru 2

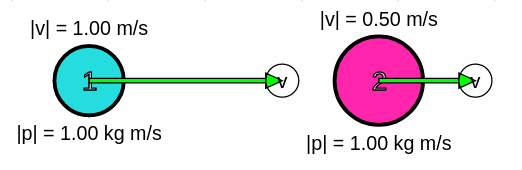
Sürtünmelerin ihmal edildiği yatay düzlemde 1kg kütleli 1 numaralı (mavi) cisim 1 m/s büyüklüğünde hız ile 2 kg kütleli (2 numaralı pembe) cisme merkezi çarpıp yapışmaktadır. Çarpışmadan sonra cisimlerin ortak hızının büyüklüğü kaç m/s olur?

Örnek

Çizgisel momentumun korunumuna göre:
\vec{p_1} + \vec{p_2} = \vec{p_t}

m_1\vec{v_1} + m_2\vec{v_2} = m_t\vec{v_t}

Değerleri yerleştirelim:
1(1) + 2(0,5) = 3\vec{v_t}

\vec{v_t} = \frac{2}{3}m/s

Hızın yönünün pozitif olduğuna, yani cisimlerin aynı yönde hareket etmeye devam ettiğine dikkat edin.

İki boyutta esnek olmayan çarpışmalar

Tıpkı bir boyutta olduğu gibi iki boyutta da esnek olmayan çarpışmalarda çizgisel momentum korunur. Bu korunumu kolayca görebilmek için momentum vektörlerini x ve y bileşenlerine ayırıyoruz. Her iki eksende de başlangıçtaki momentumun sonraki momentuma eşit olması gerekiyor. Çarpışan iki cismi ele alalım.

p_{1x} + p_{2x} = p'_{1x} + p'_{2x}

Dolayısıyla:

m_1 v_{1x} + m_2 v_{2x} = m_1 v'_{1x} + m_2 v'_{2x} p_{1y} + p_{2y} = p'_{1y} + p'_{2y}

Benzer şekilde:

m_1 v_{1y} + m_2 v_{2y} = m_1 v'_{1y} + m_2 v'_{2y}

Ama kinetik enerjinin korunmadığını hatırlayın.
E_1 + E_2 > E'_1 + E'_2

Örnek soru 3

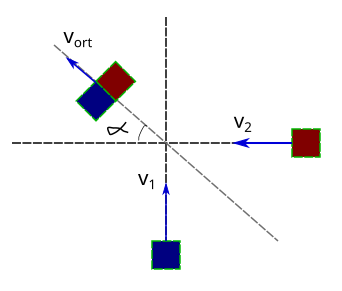
Sürtünmelerin ihmal edildiği yatay düzlem üzerinde her biri 2 kg kütleli iki cisim 12 m/s ve 16 m/s büyüklüğünde hızlarla şekildeki gibi ilerliyor. Cisimler şekilde gösterilen eksenlerin kesiştiği noktada çarpışıp kenetlendiğine göre çarpışmadan sonra cisimlerin ortak hızlarının büyüklüğü kaç m/s olur?

Çözüm

Cisimler iki boyutta tamamen esnek olmayan çarpışma yapıyor. Öyleyse çizgisel momentumun korunumunu x ve y eksenlerinde ayrı ayrı yazalım.

m_1 v_{1x} + m_2 v_{2x} = (m_1+m_2) v_{tx}

Değerleri yerlerine yazalım:
2(0)+2(-16) = 4v_{tx}

v_{tx} = -8 m/s

Aynısını y bileşenleri için de yapalım.

m_1 v_{1y} + m_2 v_{2y} = (m_1+m_2) v_{ty}

Değerleri yazalım:

2(12)+2(0) = 4v_{ty} v_{ty} = 6 m/s

Şimdi hızın büyüklüğünü bulabiliriz:
v_{t}^2 = v_{tx}^2 + v_{ty}^2

v_{t}^2 = (-8)^2 + 6^2 v_{t}^2 = 64 + 36 = 100 v_{t} = \sqrt{100} = 10 m/s

Esnek olmayan çarpışmalar ile ilgili kazanımlar

11.1.7.4. Çizgisel momentumun korunumu ile ilgili hesaplamalar yapar.

• Enerjinin korunduğu ve korunmadığı durumlar göz önüne alınarak bir ve iki boyutta çizgisel momentumun korunumu, çarpışmalar ve patlamalarla ilgili matematiksel hesaplamalar yapılması sağlanır.