Daha önce potansiyel enerjinin bir cismin veya sistemin sadece konumundan dolayı sahip olduğu enerji olduğunu öğrenmiştiniz. Potansiyel enerjisi olan bir cisim veya sistem, enerji depoladığı için, hareket etmese bile konumundan dolayı iş yapabilir. Yine daha önce kütle çekim potansiyel enerjisini öğrenmiştiniz, şimdi sırada esneklik potansiyel enerjisi var.
Aşağıdaki resimde yatay düzlemdeki bir yay denge konumuna göre önce x kadar geriliyor, sonra x kadar sıkıştırılıyor. Yaya her iki durumda da F kada bir kuvvet uygulanıyor. Eğer bir kuvvet bir cismi x kadar hareket ettiriyorsa o cisim üzerinde iş yapılyor demektir. İş varsa enerji de vardır. Bir yaya (ya da esnek başka bir cisme) kuvvet uygulayarak germe veya sıkıştırma durumunda yayda enerji depolanmasına esneklik potasiyel enerjisi denir. Bu bir enerji türü olduğu için birimi de joule (J) olur.
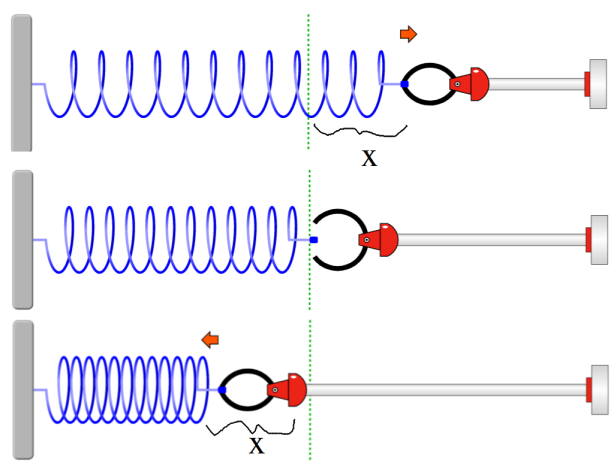
Kuvvet – uzama miktarı grafiği
Yukarıdaki resimdeki sıkışma ya da gerilme için kuvvet – yol (yer değiştirme) grafiğini çizebiliriz. Şöyle görünür:
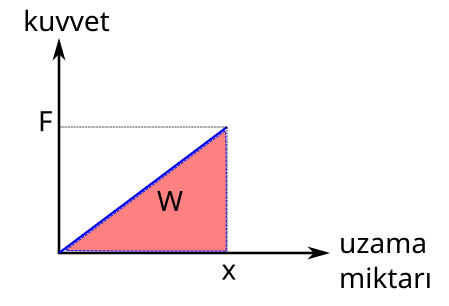
Bu grafiği yorumlayalım. Öncelikle kuvvet ile uzama (ya da sıkışma) miktarı arasındaki ilişkinin doğrusal (y = mx + b biçiminde) olduğunu görüyoruz. Kuvvet ile uzama miktarı ilşkisinin F = kx olduğunu Hooke Yasası’nda öğrenmiştiniz, bu grafiğin eğimi yay sabitini veriyor. Grafikte kuvvet ile uzama miktarı arasında kalan alana odaklanmalıyız şimdi, çünkü bu alan da bize yapılan iş miktarını verecek. Yapılan iş miktarı da yayın esneklik potansiyel enerjisine eşit olacak.
W = \frac{1}{2}Fx
F = kx ilişkisinden yerine koyalım
W = E_{p} = \frac{1}{2}(kx)x = \frac{1}{2}kx^2
Örnek soru 1
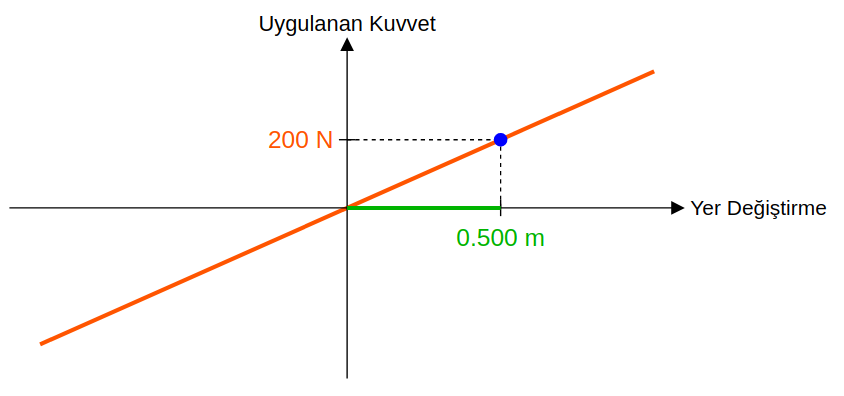
Sürtünmelerin ihmal edildiği bir ortamdaki bir yaya uygulanan kuvvet – yer değiştirme grafiği şekilde verilmiştir. Buna göre yayın uzama miktarı 0,7 m olduğunda (a) yayda depolanan esneklik potansiyel enerjisi kaç J olur? (b) Yay bu uzama miktarında cisme ne kadar kuvvet uygular?
Çözüm:
(a) Esneklik potansiyel enerjisini hesaplayabilmemiz için yay sabitini bilmemiz gerekir. Yay sabitini kuvvet – uzama miktarı grafiğinin eğiminden bulabiliriz.
k = \frac{F}{x} = \frac{200 N}{0,5 m} = 400 N/m
Yayın uzama miktarını bildiğimize göre artık esneklik potansiyel enerjisini hesaplamamız kolay:
E_p = \frac{1}{2}kx^2 = \frac{1}{2}400(N/m)(0,7 m)^2 = 98 J
(b) Yayın uyguladığı kuvveti Hooke kanununu kullanarak bulabiliriz.
F = kx
F = (400)(0,7) = 280 N
Esneklik potansiyel enerjisi – uzama miktarı grafiği
Şimdi de esneklik potansiyel enerjisinin yer değiştirmeye yani yayın uzama miktarına göre nasıl değiştiğini inceleyelim. Bunun için aşağıdaki resmi dikkatlice incelemeliyiz.
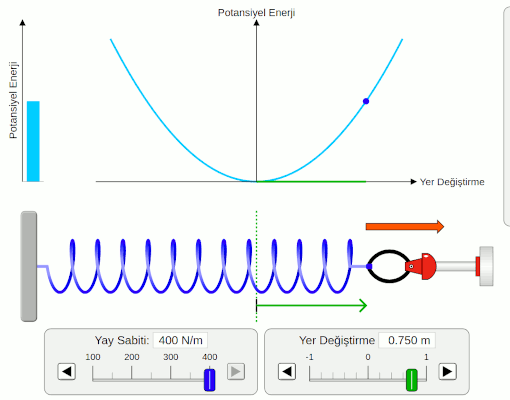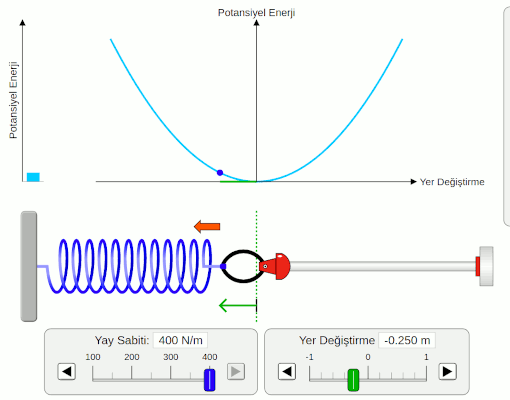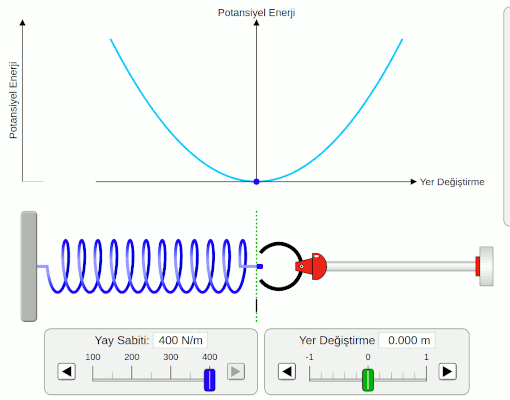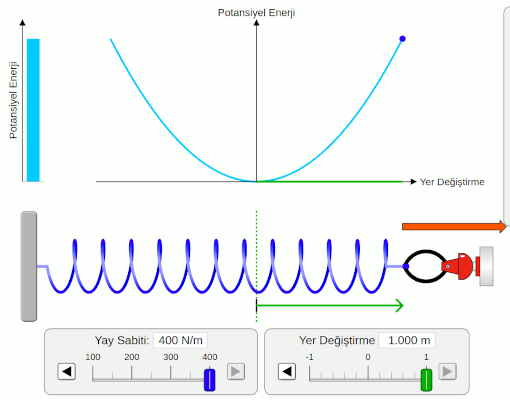
Bu resim bir simülasyondan alındı. Yay sabitini değiştirmiyoruz, hep aynı yayı kullanıyoruz. Sadece yayın uzama miktarını yani yer değiştirmesini değiştiriyoruz. Potansiyel enerjinin bir parabol olduğunu fark etmiş olmalısınız. Bunun nedeni potansiyel enerjinin uzama miktarının karesiyle doğru orantlı olması. Yayı germe ya da sıkıştırma miktarını artırdıkça, depolanan potansiyel enerji uzama miktarının karesi kadar artıyor. Yayı çok şıkıştırmanın ne kadar zor olduğunu deneyimlemiş olabilirsiniz, bu ilişki bu zorluğu açıklıyor. Ayrıca esneklik potansiyel enerjisinin hep pozitif olduğuna da dikkat edin. Yayı germek ya da sıkıştırmak potansiyel enerji açısından bir fark yaratmıyor.
Örnek soru 2
| Değişken | Ölçüm 1 | Ölçüm 2 |
|---|---|---|
| Kuvvet (N) | 40 | F |
| Potansiyel Enerji (J) | 4 | E |
| Uzama Miktarı (m) | x | 4x |
Sürtünmesiz ortamda bir yaya uygulanan kuvvet sonucunda yayın uzama ve yayda depolanan potansiyel enerji miktarları yukarıdaki tabloda verilmiştir. Buna göre (a) F kaç N, (b) E kaç J olur?
Çözüm
Soru tuhaf mı göründü? Olabilir. Ama elimizdeki kanunları bir kenara yazalım, sonra soruya saldıralım.
F = kx; E_p = \frac{1}{2}kx^2
Ölçüm 1 sütununa bakalım. Hem kuvveti hem esneklik potansiyel enerjisini biliyoruz. İkisi de uzama miktarına (x) bağlı. Buradan x’i bulabiliriz.
40 = kx
Potansiyel enerjinin kuvvete oranını deneyelim:
\frac{E_p}{F}=\frac{40}{4}=\frac{kx}{\frac{1}{2}kx^2} = \frac{2}{x}
Artık x’i bulabiliriz.
x = 2 (\frac{4}{40}) = 0,2 m
Şimdi işimiz kolaylaştı. Artık K’yı (yay sabitini) da bulabiliriz.
k = \frac{F}{x} = \frac{40}{0,2} = 200 N/m
Şimdi 4x = 4(0,2) = 0,8 m yerine koyalım ve F’yi bulalım.
F = (200 N/m)(0,8m) = 160 N
Şimdi de E’yi bulalım.
E = \frac{1}{2}(200N/m)(0,8m)^2 = 64 J
Esneklik sınırı
Hooke Yasasında bahsetmiştik burada tekrar edelim. Bir yay belli bir uzama miktarına kadar esneklik özelliğini korur, bu uzama miktarından sonra yay bozulur. Tükenmez kalem yayı bozmadıysanız, bir tane bozmanızı tavsiye ederim. Yayın bozulmadan Hooke kanununa göre davrandığı bölgeye esneklik sınırı denir. Bu bölgede uygulanan kuvvetle uzama miktarı arasındaki ilişki doğrusaldır yani F = kx şeklindedir. Esneklik potansiyel enerjisini hesaplarken de yayın hep esneklik limiti (sınırı) dahilinde davrandığını farz ettik. Eğer esneklik sınırının dışına çıkarsak esneklik potansiyel enerji burada anlattığımız şekilde hesaplanamaz.
Esneklik potansiyel enerjisi ile ilgili simülasyon
PHET’in hazırladığı Hooke Yasası simülasyonunun Enerji sekmesinde esneklik potansiyel enerjisiyle ilgili ilginç şeyler keşfedebilirsiniz. Bu yazıdaki resimler o simülasyonla hazırlandı.
Esneklik potansiyel enerjisi ile ilgili kazanımlar
11.1.6.1. Yapılan iş ile enerji arasındaki ilişkiyi analiz eder.
- Kuvvet-yol grafiğinden faydalanılarak iş hesaplamaları yapılır.
- Hooke Yasası verilir.
- Grafiklerden faydalanılarak kinetik, yer çekimi potansiyel ve esneklik potansiyel enerji türlerinin matematiksel modellerine ulaşılması sağlanır.
- Matematiksel hesaplamalar yapılması sağlanır.
Örnek soru 1’de yayın uzama miktarı fotoğrafta .5 metre ancak siz yazıda .7 demişsiniz hocam.
Grafik k, yay sabitini bulmak için kullandığımız bir araç. Soruda uzaman miktarı 0,7 m.