Hava direnci, direnç kuvveti ve limit hız nedir?

Daha önce boşlukta serbest düşen cisimlerin ve yine boşlukta yukarı ve aşağı doğru atılan cisimlerin hareketini incelemiştik. Bu atış hareketlerinin hareket denklemlerinin ve grafiklerinin bir boyutta sabit ivmeli hareketle tam olarak aynı olduklarını da görmüştük. Ama bu sonuca varmak bin yıllar almış, nedeni de yeryüzünde hareket eden cisimlerin boşlukta hareket etmemesi. Çünkü dünyanın atmosferinden dolayı cisimler yeryüzünde havanın içinde hareket ediyor, boşlukta değil. Bu yazıda havanın (aslında genel olarak akışkanların) içinde cisimlerin nasıl hareket ettiklerini anlamaya çalışacağız. Bunun için direnç kuvveti ve limit hız kavramlarını inceleyeceğiz.

Hava direnci ve direnç kuvveti nedir, nelere bağlıdır, nasıl bulunur?

Aynı yükseklikten aynı anda serbest bırakılan iki cisim boşlukta iseler, kütlelerinden ve kesit alanlarından bağımsız olarak yanyana hareket ederler. Örneğin bir demir bir gülleyle tenis topunu boşlukta aynı yüseklikten aynı anda serbest bırakırsanız ikisi de aynı anda yere düşer. Ama havanın (ya da başka bir akışkanın) içinde birlikte serbest bırakırsanız aynı anda yere düşmezler. Demir gülle tenis topundan daha önce düşer (ikisinin de küre şeklinde ve aynı büyüklükte olduklarını varsayıyoruz, dolayısıyla kesit alanları da aynı). Ama neden?

Demir gülle ve tenis topu havanın içinde hareket ederken hava tanecikleriyle çarpışır be nedenle hareket yönüne zıt yönde bir direnç kuvvetiyle karşılaşır. Eğer akışkan hava değil de su olursa, ortamın yoğunluğu arttığı için direnç kuvveti de artar. Demir güllenin, gülleyi havada bıraktığınızda, suyun içinde bıraktığınıza göre daha hızlı düştüğünü görürsünüz. Havanın uyguladığı direnç kuvveti suyunkinden daha azdır.

Hava direnci, cismin hareket doğrultusuna dik olan en büyük kesit alanı (A) ile doğru orantılıdır, kesit alan arttıkça direnç kuvveti de artar. Çünkü temas yüzeyi arttıkça cisme çarpan hava taneciği sayısı da artar.

Direnç kuvveti cismin geometrik şekline de bağlıdır. Örneğin, düz bir yüzeye göre paraşüt şeklindeki bir cisme uygulanan direnç kuvveti daha büyüktür. Çünkü hava tanecikleri paraşüte bir kez çarpıp seker sonra defalarca tekrar çarpar. Hava direnci paraşüt gibi içi boş yapılarda en büyük olur, su damlası gibi olan yapılarda ise en küçük olur. Aşağıdaki resimdeki geometrik şekillerin hava direnci sağdan sola doğru artmaktadır.

Ayrıca, direnç kuvveti ortamın direnç katsayısı (K) denen bir niceliğe de bağlıdır. Direnç katsayısı cismin şekline ve akışkanın cinsine göre değişir.

Direnç kuvveti cismin hızına bağlıdır. Çünkü cismin hızı arttıkça çarpıştığı tanecik sayısı da çarpışmaların şiddeti de artar. Direnç kuvveti cismin hızına göre hızın farklı üsleriyle doğru orantılı olabilir. Bu genel olarak şöyle ifade edilir:

F_d = KAv^n

Yeryüzüne yakın yerlerde hareket eden cisimlere etki eden direnç kuvveti için n=2 olur yani hızın karesi ile doğru orantılıdır. Bu durumda:

F_d = KAv^2

Son olarak, hava direnci cismin kütlesiyle de ilişkilidir. Cismin kütlesi arttıkça direnç kuvveti de artar. Bunu önce bir örnekle açıklayalım sonra matematiksel olarak türetilmesini limit hızı anlattıktan sonra gösterelim. Elimizde iki pinpon topu olsun. Birinin içini boş bırakalım, diğerinin içine şırıngayla su dolduralım. Şimdi bu iki pinpon topunu aynı yükseklikten aynı anda bırakırsak hangisi daha önce yere düşer? Su dolu olan, isterseniz bunu evde deneyebilirsiniz. Aynısını bir tenis topu ve demir gülle için de düşünebiliriz.

Limit hız nedir, nasıl bulunur?

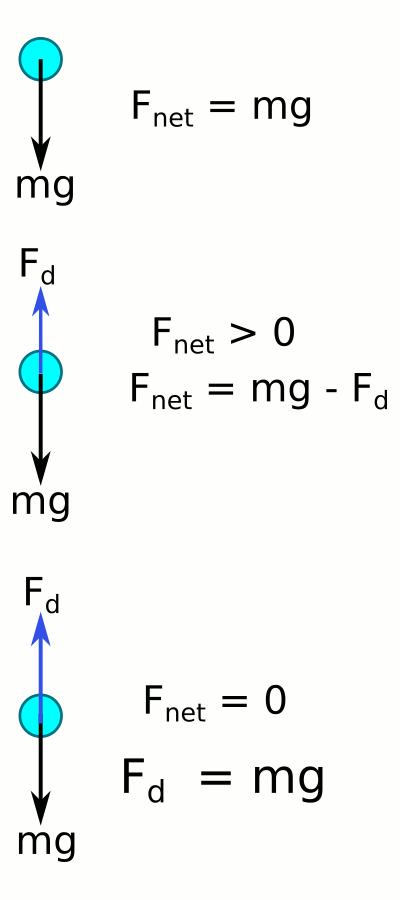
Hiç düşündünüz mü, yağmur damlaları kilometrelerce yüksekten düşmelerine rağmen neden canımızı acıtmaz? Bir yağmur damlasının düşerken ki serbest cisim diyagramlarını çizip inceleyelim.

Yağmur damlası buluttan düştüğü anda üzerindeki net kuvvet damlanın ağırlığına eşittir. İlk durumda, damla Newton’un ikinci hareket kanununa göre ivmelenir, yani hızı artar. Ama hızı arttıkça damlaya uygulanan direnç kuvveti de artmaya başlar. İkinci durumda net kuvvet azalır dolayısıyla ivme azalmaya başlar, damla hızlanmaya devam eder ama hız artışı daha az olur. Bir süre sonra damlanın hızı direnç kuvvetinin damlanın ağırlığına eşit olacağı duruma ulaşır. (F_d = mg). Bu durumda damlaya etki eden net kuvvet sıfır olur, dolayısıyla Newton’un birinci hareket kanununa göre damla sabit hızla hareket eder. İşte bu hıza limit hız (v_lim) adı verilir.

Limit hızın matematik modelini birlikte çıkaralım:

F_d = G F_d = KAv_{lim}^2; G=mg KAv_{lim}^2 = mg v_{lim}^2 = \frac{mg}{KA} v_{lim} = \sqrt{\frac{mg}{KA}}

İçi su dolu olan pinpon topunun boş olandan daha önce düşmesinin matematiksel nedenini anlayabildiniz mi?

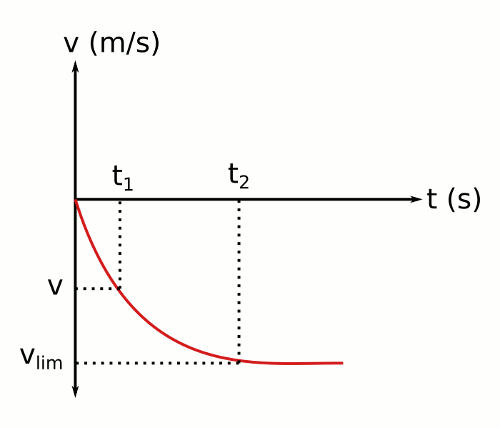
Şimdi bir de hava direncinin olduğu ortamda serbest bırakılan bir cismin hız – zaman grafiğine bakalım. Bu grafiğe göre cisim önce hızlanıyor sonra limit hıza ulaşınca sabit hızla hareket etmeye devam ediyor.

Günlük yaşamda hava direnci ve limit hız

Kilometrelerce yüksekten düşen yağmur damlalarının canımızı yakmamasının nedeni hava direncidir. Ayrıca dolu tanelerinin de vereceği zararı azalmasının nedeni limit hıza ulaşmalarıdır. Paraşütle atlayarak zarar görmeden yere inilebilmesi de yine hava direncine bağlıdır. Ama hava direnci hızlı gitmesini istediğimiz araba, tren ve uçak gibi taşıtların daha fazla yakıt tüketmesine de neden olur.

Örnek Soru

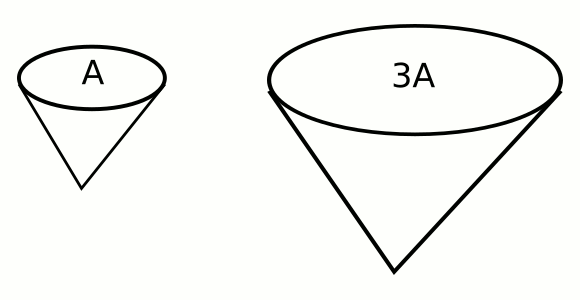
Aşağıdaki resimde kütleleri eşit iki koni şeklinde cisim gösteriliyor. Soldaki koninin taban alanı A, sağdakinin 3A’dır. Buna göre koniler limit hıza ulaşabilecekleri aynı yükseklikten serbest bırakıldıklarında göre hangi koni daha önce yere düşer?

Çözüm

Hava direnci, cismin hareket doğrultusundaki en büyük kesit alanına, şekline ve içinde bulunduğu akışkanın cinsine bağlı olarak değişir. Direnç kuvvetiyle cismin ağırlığı eşitlendiğinde cisim limit hıza ulaşır. İki koni de aynı ortamda bulunan eşit kütleli cisimler olduğu için hava direncini etkileyen tek değişken konilerin en büyük kesit alanıdır. Sağdaki koninin taban alanı (en büyük kesit alanı) 3A, soldaki A olduğu için, sağdaki koniye etkiyen direnç kuvveti daha büyüktür, dolayısıyla limit hıza daha çabuk ulaşır. Bu nedenle soldaki cisim yere daha önce düşer.

Hava direnci ve limit hız ile ilgili kazanımlar

11.1.4.4. Düşen cisimlere etki eden hava direnç kuvvetinin bağlı olduğu değişkenleri analiz eder.

• Öğrencilerin değişkenleri deney yaparak veya simülasyonlar kullanarak belirlemeleri sağlanır.

11.1.4.5. Limit hız kavramını açıklar.

• Limit hız kavramı günlük hayattan örneklerle (yağmur damlalarının canımızı acıtmaması vb.) açıklanır.
• Limit hızın matematiksel modeli verilir. Matematiksel hesaplamalara girilmez.