İş ve enerji arasındaki ilişki nedir? Örnek soru çözümleri

Enerjinin iş yapabilme yeteneği olduğunu söylemiştik. Öyleyse enerji ve iş arasında bir ilişki olmalı. Bir cismin üzerinde iş yaparsanız o cismin enerjisini artırırsınız ya da azaltırsınız. Enerjideki değişim miktarı yapılan işe eşittir. İşi tanımlarken enerji aktarımının bir yoludur demiştik. Bir cismin enerjisini başka bir cisme kuvvet aracılığıyla aktardığınızda, enerji transfer mekanizması iş olur. İş enerjinin aktarımıdır. Bir cisim başka bir cisim üzerinde iş yaparsa enerjisi azalır; iş yaptığı cismin ise enerjisi artar.

Örneğin aşağıdaki resimde bir adam bir kaykayın üstündeki kutuyu itiyor, kutunun üstünde iş yapıyor. Adamın enerjisi azalır, kutunun enerjisi artar. Adamın enerjisi kutuya iş aracılığıyla aktarılır.

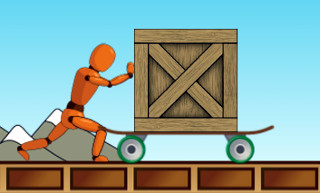
Yapılan iş ve enerji aktarımının yönü

İş nedir sorusunu yanıtlarken yapılan işin artı ya da eksi olabileceğini görmüştük. Eğer iş artı işaretli olursa cisim enerji kazanır. İş eksi işaretli olursa cisim enerji kaybeder. Aşağıdaki örneklerde bu durum gösteriliyor.

Yapılan iş ve kinetik enerji değişimi

Bir cismin kütle çekim potansiyel enerjisini değiştirmeden üzerinde iş yaparsanız yalnızca kinetik enerjisini değiştirirsiniz. Örneğin:

• Doğrusal bir yolda bir cisme kuvvet uygulayarak hareket ettirmek
• Yüksekliğini değiştirmeden bir cisim üzerinde iş yapmak
  yalnızca cismin kinetik enerjisini değiştirir.

Kinetik enerji iş teoremi denen bu ilkenin matematiksel gösterimi şöyledir:

W = ∆KE = KE_son – KE_ilk

Son kinetik enerjiden ilk kinetik enerjiyi çıkardığınızda bulduğunuz değişim miktarıdır, bu da yapılan işe eşittir.

Örnek soru 1 – Pedal çevirip hızlanan bisikletli

Bir bisikletli düz bir yolda dururken pedal çevirmeye başlayıp hızını 8 m/s’ye çıkarıyor. Bisikletle birlikte bisikletlinin kütlesi 75 kg olduğuna göre yapılan iş kaç J’dür?

Çözüm:

Bisikletlinin düz bir yolda ilerlemesi yokuş çıkmaması ya da inmemesi demek. Yani potansiyel enerjisi değişmemiş, yalnızca kinetik enerjisi değişmiş.

W = ∆KE

∆KE = KE_son – KE_ilk

KE_son = 1/2mv_son²

v_son = 8 m/s

KE_son = 1/2(75 kg)(8 m/s)²

KE_son = 2400 J

KE_ilk = 1/2mv_ilk²

v_ilk = 0 m/s

KE_ilk = 1/2(75 kg)(0 m/s)² = 0 J

∆KE = 2400 J – 0 J = 2400 J

W = +2400 J

Bisikletli pedal çevirirken bisiklete kuvvet uyguladı ve yer değiştirmesini sağladı. Aynı zamanda hızını da artırdı. Kinetik enerjisindeki değişim yaptığı işe eşit. İşin işaretinin artı olması bisikletin enerjisinin arttığını yani hızlandığını gösteriyor. Bisiklete enerji aktarılmış anlamına geliyor.

Ayrıca yapılan işin sebebi hem pedal çeviren bisikletlinin uyguladığı kuvvet hem de bisikletle yer arasındaki sürtünme kuvveti. Bisikletlinin uyguladığı kuvvetin yaptığı pozitif iş, sürtünme kuvvetinin yaptığı negatif iş. Bisiklet hızlandığı için yapılan net iş pozitif.

Örnek soru 2 – Frene basıp yavaşlayan bisikletli

Bir bisikletli düz bir yolda 8 m/s hızla ilerlerken frene basıp hızını 2 m/s’ye düşürüyor. Bisikletle birlikte bisikletlinin kütlesi 75 kg olduğuna göre yapılan iş kaç J’dür?

Çözüm:

Bu kez bisikletli frene basmış, bisiklet yavaşlamış. Ama kinetik enerjinin değişimi hala yapılan işe eşit olmak zorunda.

W = ∆KE

∆KE = KE_son – KE_ilk

KE_son = 1/2mv_son²

v_son = 2 m/s

KE_son = 1/2(75 kg)(2 m/s)²

KE_son = 150 J

KE_ilk = 1/2mv_ilk²

v_ilk = 8 m/s

KE_ilk = 1/2(75 kg)(8 m/s)² = 2400 J

∆KE = 150 J – 2400 J = -2250 J

W = -2250 J

Bisikletli fren yaptığı zaman bisiklete uyguladığı kuvvetin yönü, hareket yönünün zıttı. Bu nedenle bisikleti yavaşlattı, hızını azalttı. Kinetik enerjideki değişim yapılan işe eşit. İşin işaretinin eksi olması bisikletin enerjisinin azaldığını yani yavaşladığını gösteriyor. Bisikletten enerji aktarılmış demek. Fren yapmak tamamen sürtünme kuvvetinin etkisi demek. Bu nedenle yapılan iş negatif oldu.

Yapılan iş ve potansiyel enerji değişimi

Bir cismin kinetik enerjisini değiştirmeden üzerinde iş yaparsanız yalnızca potansiyel enerjisini değiştirirsiniz. Örneğin:

• Başlangıçta duran bir cismi yukarı kaldırmak veya aşağı indirmek, sonunda da cismin yine durması
• Sabit hızla bir cismi yukarı kaldırmak ya da aşağı indirmek, cismin hızının hiç değişmemesi
  cismin sadece potansiyel enerjisini değiştirir.

Yapılan iş yer çekimi potansiyel enerjisindeki değişime eşit olur. Matematiksel olarak şöyle gösterebiliriz:

W = ∆PE = PE_son – PE_ilk

Son potansiyel enerjiden ilk potansiyel enerjiyi çıkardığınızda enerjideki değişim miktarını elde edesiniz, bu da yapılan işe eşittir.

Örnek soru 3 – Üst kata çıkan asansör

Kütlesi 800 kg olan bir asansör zemin kattan 9 m yükseklikteki üçüncü kata çıktığına göre asansör üzerinde yapılan iş kaç J’dür? Asansör zemin katta ve üçüncü katta durmuştur.

Çözüm:

Asansörün ilk ve son hızlarının sıfır olduğunu biliyoruz. Bu nedenle kinetik enerjide değişim yok. Sadece potansiyel enerji değişmiş.

W = ∆PE

∆PE = PE_son – PE_ilk

PE_son = mgh_son

h_son = 9 m

PE_son = (800 kg)(10 m/s²)(9 m)

PE_son = 72000 J

PE_ilk = mgh_ilk

h_ilk = 0 m

PE_ilk = (800 kg)(10 m/s²)(0 m) = 0 J

∆PE = 72000 J – 0 J = +72000 J

W = +72000 J

Yapılan işin işareti artı, bu nedenle asansör potansiyel enerji kazanmış.

Örnek soru 4 – Yük indiren vinç

Bir vinç kütlesi 200 kg olan bir yükü sabit hızla 18 m yükseklikten 4 m yüksekliğe indirdiğine göre yapılan iş kaç J’dür?

Çözüm:

Vinç yükü indirirken yükün hızı değişmemiş. Öyleyse yapılan iş kütle çekim potansiyel enerijsindeki değişime eşit olmalı.

W = ∆PE

∆PE = PE_son – PE_ilk

PE_son = mgh_son

h_son = 4 m

PE_son = (200 kg)(10 m/s²)(4 m)

PE_son = 8000 J

PE_ilk = mgh_ilk

h_ilk = 18 m

PE_ilk = (200 kg)(10 m/s²)(18 m)

PE_ilk = 36000 J

∆PE = 8000 J – 36000 J = -28000 J

W = -28000 J

Yapılan işin işareti eksi, bu nedenle yük potansiyel enerji kaybetmiş.

Yapılan iş ve mekanik enerji değişimi

Bir cismin üzerinde yapılan iş aynı anda cismin hem kinetik hem de potansiyel enerjisini değiştirebilir. Bu durumda yapılan iş mekanik enerjideki değişime eşittir. Matematiksel olarak şöyle gösterebiliriz:

W = ∆ME = ME_son – ME_ilk

∆ME = ∆KE + ∆PE

W = ∆KE + ∆PE

W = (KE_son – KE_ilk) + (PE_son – PE_ilk)

Örnek soru 5 – Üst kata çıkarken hızlanan asansör

Kütlesi 800 kg olan bir asansör zemin katta dururken harekete başlayıp 12 m yükseklikteki dördüncü kata ulaştığında hızı 2 m/s oluyor. Asansörün üzerinde yapılan iş kaç J’dür?

Çözüm:

Asansör başlangıçta duruyormuş sonra hızlanmış, yani kinetik enerjisi değişmiş. Ayrıca asansör önce zemin kattaymış sonra 12 m yüksekliğe çıkmış, yani potansiyel enerjisi de değişmiş. Öyleyse mekanik enerjisindeki değişimi hesaplarsak yapılan işi de buluruz.

W = ∆ME = ME_son – ME_ilk

∆ME = ∆KE + ∆PE

W = ∆KE + ∆PE

W = (KE_son – KE_ilk) + (PE_son – PE_ilk)

Önce kinetik enerjideki değişimi bulalım:

KE_son = 1/2mv_son²

v_son = 2 m/s

KE_son = 1/2(800 kg)(2 m/s)²

KE_son = 1600 J

KE_ilk = 1/2mv_ilk²

v_ilk = 0 m/s

KE_ilk = 1/2(75 kg)(0 m/s)² = 0 J

∆KE = 1600 J – 0 J = 1600 J

Şimdi de potansiyel enerjideki değişimi bulalım:

∆PE = PE_son – PE_ilk

PE_son = mgh_son

h_son = 12 m

PE_son = (800 kg)(10 m/s²)(12 m)

PE_son = 96000 J

PE_ilk = mgh_ilk

h_ilk = 0 m

PE_ilk = (800 kg)(10 m/s²)(0 m) = 0 J

∆PE = 96000 J – 0 J = +96000 J

Artık yapılan işi yani mekanik enerjideki değişimi bulabiliriz:

W = ∆KE + ∆PE

W = 1600 J + 96000 J = 97600 J

İş ve enerji ilişkisi ile İlgili Kazanımlar

9.4.1.1. İş, enerji ve güç kavramlarını birbirleriyle ilişkilendirir.

• İş ile enerji arasındaki ilişki kavramsal olarak verilir.