Kasnak nedir? Örnek Sorular ve Çözümleri

Kasnak, bir merkez etrafında dönebilen ve etrafına kayış sarılabilen basit makinelere verilen addır. Farklı kasnaklar birbirine kayışlarla bağlanır. Böylece tıpkı çarklar ve dişlilerde olduğu gibi birbiriyle uyum içinde çalışarak enerji aktarımını sağlayan makine sistemleri oluşturulur. İki kasnak birbirine farklı şekillerde bağlanabilir. Bağlanma biçimlerine göre kasnakların birbirine göre dönme yönlerini inceleyelim.

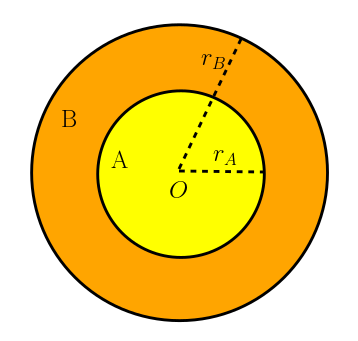
Yukarıdaki şekilde A kasnağı (içerideki küçük sarı olan), B kasnağıyla eş merkezli (çakışık eksenli) olacak biçimde bağlanmış. Yarıçapları farklı olsa da küçük kasnak bir tur attığı zaman, büyük kasnak da ona bağlı olduğu için büyük kasnak da bir tur atar. Yani tur sayıları birbirine eşit olur. n_A = n_B.

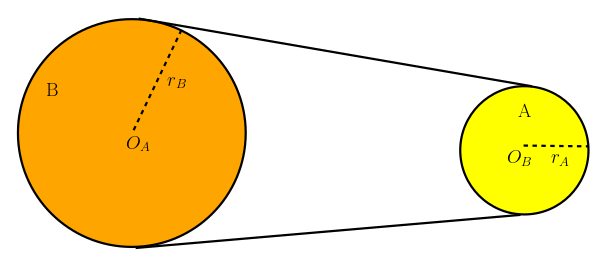
Yukarıdaki şekilde A kasnağıyla B kasnağı bir kayışla düz bağlanmış. Bisiklet zinciri gibi. Bu kasnakların aynı yönde döneceğini görebildiniz mi? B kasnağı saat yönünde dönerse, A kasnağı da saat yönünde döner.

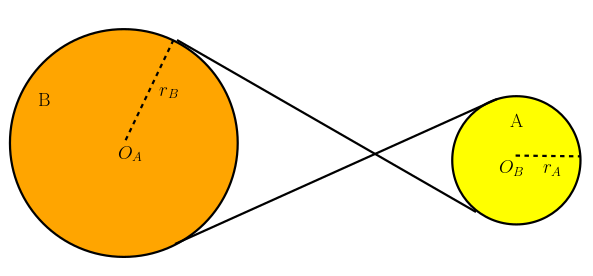
Son bağlanma biçimi olarak, yukarıdaki şekilde gösterilen, A kasnağının B kasnağına bir kayışla çapraz bağlandığı duruma bakalım. Bu iki kasnağın zıt yönde döneceğini görebildiniz mi? B kasnağı saat yönünde dönerse, A kasnağı saat yönünün tersinde döner.

Şimdi de kayışla bağlanan kasnakların tur sayılarını inceleyelim. Hem düz hem çarpraz bağlanan iki kasnağı ele alacağız. Çünkü tur sayıları her iki durumda da aynı. Öncelikle kayış üstünde her noktanın gerilme kuvveti aynıdır. Enerjinin korunumuna göre B kasnağı üzerinde yapılan iş, A kasnağına aktarılan enerjiye eşit olmalı. Öyleyse:
W_B = F x_B

B kasnağı n_B kadar tur attığı zaman aldığı yol tur sayısıyla B kasnağının çevresinin çarpımına eşit:
x_B = n_B(2 \pi r_B)

W_B = 2\pi F n_B r_B

Aynı durum A kasnağı için de geçerli:
W_A = F x_A; \space x_A = n_A(2 \pi r_A)

W_A = 2\pi F n_A r_A

Şimdi yapılan işleri eşitleyelim:
W_A = W_B

2\pi F n_B r_B = 2\pi F n_A r_A n_B r_B = n_A r_A \frac{n_A}{n_B} = \frac{r_B}{r_A}

Sonucumuzu yorumlayalım: A ve B kasnaklarının tur sayıları yarıçaplarının büyüklüğüyle ters orantılı.

Örnek soru 1

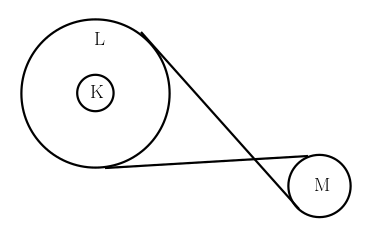
Şekilde gösterilen sistemde K, L ve M kasnaklarının yarıçapları sırasıyla r, 4r ve 2r’dir. Buna göre K kasnağı saat yönünde 2 tur atarsa M kasnağı hangi yönde kaç tur atar?

Çözüm

Öğrendiklerimizi uygulayalım. Önce K ve L kasnaklarına bakalım. Bunlar eşmerkezli. Yani K ile L aynı yönde dönüyor (saat yönünde) ve tur sayıları aynı. Demek ki n_K = n_L = 2.

Şimdi L ile M’ye bakalım. Bu iki kasnak birbirine çapraz bağlanmış demek ki zıt yönde dönüyorlar. Demek ki M kasnağı saat yönünün tersi yönde dönüyor. Şimdi de tur sayısını hesaplayalım:
\frac{n_M}{n_L} = \frac{r_L}{r_M}

n_M = 2 \frac{4r}{2r} = 4

Yani M kasnağı saat yönünün tersinde 4 tur dönüyor.

Örnek soru 2

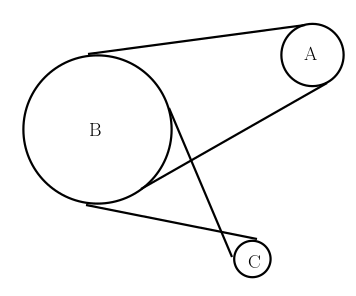
Şekilde gösterilen sistemde A, B ve C kasnaklarının yarıçapları sırasıyla 3r, 4r ve r’dir. Buna göre A kasnağı saat yönün tersinde 5 tur atarsa C kasnağı hangi yönde kaç tur atar?

Çözüm

Bu kez üç kasnak var. Kaç kasnak olduğu pek önemli değil, yeterki adım adım gidelim ve yolumuzu kaybetmeyelim. Bize verilenden başlayalım yani A kasnağından. A ile B birbirine düz bağlanmış demek ki ayn yönde dönüyorlar (saat yönünün tersinde). Şimdi tur sayılarına bakalım.
\frac{n_A}{n_B} = \frac{r_B}{r_A}

\frac{5}{n_B} = \frac{4r}{3r} n_B = 5 \times \frac{3}{4} = \frac{15}{4}

Tuhaf bir tur sayısı ama dursun. Şimdi C kasnağına bakalım. B ile C birbirine çapraz bağlanmış öyleyse zıt yönde dönüyorlar. Demek ki C saat yönünde dönüyor. Şimdi de tur sayısını bulalım.
\frac{n_B}{n_C} = \frac{r_C}{r_B}

\frac{\frac{15}{4}}{n_C} = \frac{r}{4r} n_C = \frac{15}{4}(4) = 15

C kasnağının saat yönünde 15 tur attığını bulduk. Bu soruları çözerken işlem hatası yapmamaya dikkat etmeniz gerekiyor.

Kasnaklarla ilgili Kazanımlar

11.1.10.1. Günlük hayatta kullanılan basit makinelerin işlevlerini açıklar.

• Kaldıraç, sabit ve hareketli makara, palanga, eğik düzlem, vida, çıkrık, çark ve kasnak ile sınırlı kalınır.

11.1.10.2. Basit makineler ile ilgili hesaplamalar yapar.

• İkiden fazla basit makinenin bir arada olduğu sistemlerle ilgili matematiksel hesaplamalara girilmez.
• Hesaplamaların günlük hayatta kullanılan basit makine örnekleri (anahtar gibi) üzerinden yapılması sağlanır.
• Basit makinelerde verim ile ilgili matematiksel hesaplamalar yapılması sağlanır.