Elektrik devrelerini analiz etmek için, her devre elemanının üstündeki akımı ve potansiyel farkı bilmek gerekir. Kirchoff kanunları (Kirchoff kanunu, yasası, yasaları veya kuralları da denir), belirli bir anda bir elektrik devresindeki akımların sağlaması gereken koşulları veren iki ilkeye denir. 19. yüzyılda Alman bilim insanı Gustav Kirchhoff tarafından keşfedildiği için, onu onurlandırmak için, bu kanunlara onun adı verilmiştir. Kirchoff kanunları yükün korunumuna ve enerjinin korunumuna dayanır. Devre yapım seti simülasyonunu kullanarak bu Kirchoff yasalarını inceleyelim.
1. Kirchoff kanunu: Düğüm kuralı veya akım kanunu
Kirchoff’un ilk kanunu bir elektrik devresindeki akımların nasıl davrandığını açıklar. Bu Kirchoff kanununa göre, bir devrede bir düğüm noktasına (kavşak veya birleşme noktasına) gelen akımların toplamı, düğüm noktasından çıkan (bu noktayı terk eden) akımların toplamına eşit olmak zorundadır. Bunu nereden biliyoruz? Elektrik yükünün korunduğunu, yoktan yük yaratılamayacağını ve var olan yükün yok edilemeyeceğini, dolayısıyla toplam yük miktarının sayısının değişmeyeceğini elektrik yükleri konusunda öğrenmiştik.
Aşağıdaki resimde bir düğüm noktasına (üç telin birleştiği gri noktaya) iki koldan akım geliyor ve bir koldan akım çıkıyor. Çıkan akım bu noktadan geçen yüklerin miktarının zamana oranıdır. Bu noktaya gelen yüklerde yalnızca giren birinci ve ikinci koldan geldiğine göre, çıkan kolda birim zamanda geçen yük miktarı, giren kollardaki birim zamanda geçen yük miktarına eşit olmak zorundadır.
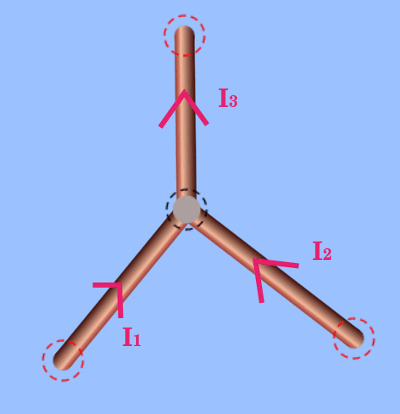
Dolayısıyla I3 = I1 + I2 olmak zorundadır.
Aşağıdaki resimde bu kez bir koldan gelen akımın ikiye dağılması gösteriliyor.
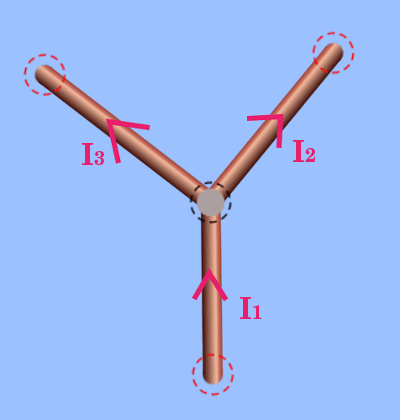
Bu durumda da yine Kirchoff kanunu geçerlidir: I1 = I2 + I3
Bunu genellersek, bir elektrik devresindeki herhangi bir düğüm noktası için, giren akımların toplamı çıkan akımların toplamına eşittir:
ΣIgiren = ΣIçıkan
2. Kirchoff kanunu: Çevrim kuralı veya Voltaj kanunu
Kirchoff’un ikinci kanunu kapalı bir elektrik devresinde bütün devre elemanlarının uçları arasındaki potansiyel fark toplamlarının sıfır olmak zorunda olduğunu söyler. Elektrik potansiyelin önemli bir özelliği kapalı bir döngüde potansiyel fark toplamının sıfır olmasıdır. Bu enerjinin korunumundan gelir. Çünkü bir elektrik yükü bir devrede başladığı noktaya gelirse yükün potansiyel enerjisindeki değişim sıfır olur, dolayısıyla potansiyelindeki değişim de sıfır olur. Bu fikri bir elektrik devresine uyguladığımızda tüm devre elemanlarının potansiyel fark toplamlarının sıfır olması gerektiği sonucuna ulaşırız.
∆Vkapalı devre = 0
∆Vkapalı devre = ∆V1 + ∆V2 + .. + ∆ Vn = 0
∆Vkapalı devre = Σ∆V = 0
Kirchoff’un ikinci kanunu bir örnek üzerinde görelim. Aşağıdaki resim basit bir elektrik devresindeki, potansiyel farkları sırasıyla V1, V2 ve V3 olan üç pili ve dirençleri sırasıyla R1, R2 ve R3 olan üç direnci gösteriyor.
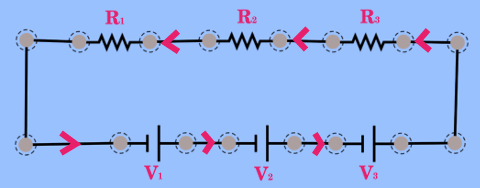
Kirchoff’un çevrim kanunu ancak devre elemanlarından en az birinin potansiyel farkının eksi (negatif) olmasıyla mümkündür. Hepsi artı olursa, sonuç sıfır çıkamaz. Bu nedenle hangi devre elemanlarının uçları arasındaki potansiyel farkın eksi olduğunu açıkça belirlememiz gerekir. Bu konuda şu kurallar işimizi kolaylaştırır:
- İdeal (direnci sıfır kabul edilen) bir telin üstündeki iki noktanın potansiyeli aynıdır, dolayısıyla telin üstündeki bu iki nokta arasındaki potansiyel fark sıfırdır.
- Akımın yönü bir üretecin (pilin) eksi kutbundan (ucundan) artı kutbuna doğru ise pilin potansiyel farkı (voltajı veya gerilimi) artı (pozitif) olarak alınır. Devre gösteriminde pildeki kısa çizgi eksi kutbu, uzun çizgi artı kutbu gösterir. ∆Vüreteç = ε olarak alınır. ε pilin elektromotor kuvveti (EMK’sı) anlamına gelir.
- Akımın yönü bir üretecin artı kutbundan eksi kutbuna doğru ise pilin potansiyel farkı eksi (negatif) olarak alınır. ∆Vüreteç = -ε olarak alınır.
- Herhangi bir direncin üstünden geçen akımın yönü ne olursa olsun direncin potansiyel farkı eksi (negatif) olarak alınır.
Ohm kanunu bize sadece bir direncin üstündeki potansiyel farkın büyüklüğünü (şiddetini) verir. Kirchoff kanunu ise direncin uçları arasındaki potansiyel farkın akımın geçtiği yönde azalmak zorunda olduğunu fark etmeye zorlar. Bir direncin uçları arasında voltaj daima düşer. Elektrik akımı daima yüksek potansiyelden düşük potansiyele doğru akar.
Yukarıdaki resmi analiz edip artık Kirchoff’un ikinci kanunu yazabiliriz:
∆Vkapalı devre = Σ∆V = 0
∆Vkapalı devre = V1 + V2 + V3 – IR1 – IR2 – IR3 = 0
V1 + V2 + V3 = I(R1 + R2 + R3 )
Kirchoff kanunları örnek soru 1
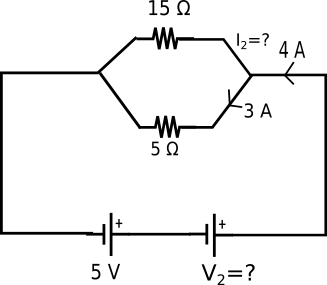
Yukarıdaki şekilde biri 5 V olan diğerinin potansiyel farkı bilinmeyen iki pil ve sırasıyla dirençleri 15 ohm ve 5 ohm olan iki direnç bir elektrik devresi oluşturmak üzere bağlanmıştır. İkinci pilden çıkan akım 4 amper ve 5 ohmluk direncin üstünden geçen akım 3 amper olduğuna göre:
a) 15 ohmluk direncin üstünden geçen akım I2 kaç amperdir?
b) İkinci pilin potansiyel farkı V2 kaç volttur?
Çözüm:
A şıkkını çözmek için Kirchoff’un akımlar kanunu kullanabiliriz. Bir düğüm noktasına giren akımların çıkan akımlara eşit olması gerekir. Öyleyse:
4 A = 3 A + I2
I2 = 4 A – 3 A = 1 A
B şıkkını çözmek için Kirchoff’un voltaj kanununu kullanabiliriz. Kapalı devre boyunca toplam potansiyel farkın sıfır olması gerekir. Dikkat etmemiz gereken en önemli nokta, dirençlerin başladığı düğüm noktasıyla dirençlerin bittiği düğüm noktası arasındaki potansiyel farkın, yalnızca bir direncin potansiyel farkına eşit olduğu. Çünkü dirençlerin başladığı noktanın potansiyeli her iki direnç için de aynı; dirençlerin bittiği noktanın da potansiyelleri aynı. Ayrıca iki direncin potansiyel farklarının da birbirine eşit olduğunu Ohm kanunundan görebiliriz:
∆VR1 = 1 A . 15 Ω = 15 V
∆VR2 = 3 A . 5 Ω = 15 V
Artık Kirchoff’un çevrim kanunu yazabiliriz:
∆Vkapalı devre = Σ∆V = 0
5 V + V2 – 3 A . 5 Ω = 0
V2 + 5 V – 15 V = 0
V2 – 10 V = 0
V2 = 10 V
Kirchoff kanunları örnek soru 2
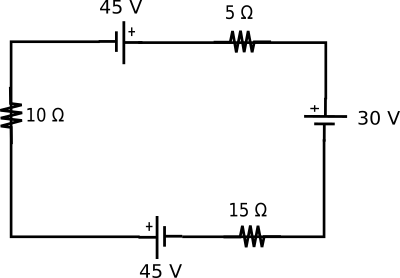
Yukarıdaki şekilde gösterilen kapalı devrede, devreden geçen akım kaç amperdir?
Çözüm:
Elimizde bir tane kapalı döngü var. Düğüm noktası yok, kol yok, kavşak yok. Öyleyse devrenin her noktasından aynı akım geçmek zorunda. Alttaki 45 V’luk pilden çıkan akım artı ucundan başlayıp sola doğru devam edecek. Akımın yönünü belirledikten sonra tek yapmamız gereken Kirchoff’un gerilim kanunun yazmak.
∆Vkapalı devre = Σ∆V = 0
45 V – I10 Ω + 45 V – I5 Ω – 30 V – I15 Ω = 0
Dikkat etmeniz gereken en önemli nokta 30 V’luk pilin potansiyel farkını eksi olarak yazmış olmamız. Çünkü pil akıma ters yönde bağlanmış, akım artı ucundan giriyor. Diğer pillerde ise akım pillerin eksi ucundan giriyor artı ucundan çıkıyor, diğer piller doğru bağlandığı için onların potansiyel farklarını artı olarak aldık.
45 V + 45 V – 30 V – I(10 Ω + 5 Ω + 15 Ω) = 0
60 V – I30 Ω = 0
60 V = I30 Ω
I = 2 A
Kirchoff kanunları ile ilgili kazanımlar
2013 – 10.2.3.3. Kirchoff’un akımlar ve gerilimler kanunlarını açıklar.
- Kirchoff kanunları ile ilgili matematiksel işlemlere girilmez.
Merhaba, öncelikle bu anlaşılır ve mantığı irdeleyen anlatımınız için sizi kutlarım, fakat bu konuda 2. Kuralda v lerin hepsinin toplam olması gerekirken v2 ve v3 arasında artı koymayı unutmuşsunuz sanırım. Bir de 4 kuraldan bahsetmişsiniz fakat bu kuralların 2. si ve 3. sünde tamamen aynı şeyleri yazmanıza rağmen birinde pozitif diğerinde negatif yazmışsınız. Henüz bu kanunları yeni öğrendiğim için yanlış bi tespit yapmış olabilirim, fakat doğruysa kafa karışıklığını önlemek için düzeltmenizi rica ediyorum. Saygılar.
Armağan, V2 ve V3 arasına + işaretini unutmuşum, ekledim, dikkatin harika. Dört kuralda 2. ve 3. aslında aynı sadece üretecin bağlanma yönüne göre değerini artı mı eksi mi almak gerektiğini açık açık söylüyor.
İlginiz ve cevabınız için teşekkür ederim. Yalnız, dediğinize ve soru çözümünüze göre 3. Kuralda artı kutbundan eksi kutbuna doğru ise potansiyel fark negatif olması gerekiyor o zaman. İkisinde de üreteçlerin yönünü aynı yazdığınıza dikkat etmenizi öneririm. Saygılar.
İki soruda da üreteçler aynı yönlü (ters olmayacak şekilde) bağlanmış zaten. İlk soruda zaten net, ikinci soruda saat yönünde döngü yapıp Kirchoff kanunlarını yazıyoruz.
Hocam arkadaş sorudan bahsetmemiş bence.Kirchoff kanununu anlattığınız 4 öncüllü yerdeki 2. ve 3. maddeyi kastetmiş.
3.Akımın yönü bir üretecin eksi kutbundan artı kutbuna doğru ise pilin potansiyel farkı eksi (negatif) olarak alınır. ∆Vüreteç = -ε olarak alınır.
_ Bu cümlenin “Akımın yönü bir üretecin artı kutbundan eksi kutbuna doğru…..” şeklinde olması gerekmiyor mu?
Hocam şu iki maddede bir kavram karışıklığı yok mu?
1 Akımın yönü bir üretecin (pilin) eksi kutbundan (ucundan) artı kutbuna doğru ise pilin potansiyel farkı (voltajı veya gerilimi) artı (pozitif) olarak alınır. Devre gösteriminde pildeki kısa çizgi eksi kutbu, uzun çizgi artı kutbu gösterir. ∆Vüreteç = ε olarak alınır. ε pilin elektromotor kuvveti (EMK’sı) anlamına gelir.
2 Akımın yönü bir üretecin eksi kutbundan artı kutbuna doğru ise pilin potansiyel farkı eksi (negatif) olarak alınır. ∆Vüreteç= -ε olarak alınır.
Çok güzel yakalamışsınız. Düzeltildi. 2. maddede “pilin artı kutbundan eksi kutbuna doğru” olacak.