Bu uzun bir yazı, isterseniz sadece videoları izleyebilirsiniz. Newton’un ikinci hareket yasası, Newton’un hareket yasalarının merkezindedir, dinamiğin temel yasası ya da temel prensip olarak da adlandırılır. F=ma olarak ünlenmiştir.
Newton’un ikinci hareket yasasının özü: kuvvetin hareket üzerindeki etkisi
Duran bir cismi harekete geçirmek için kuvvet gerekir. Sabit hızla giden bir cismin hızını değiştirmek için de kuvvet gerekir. Daha genel bir ifadeyle bir cismin hareket durumunu yani hızını değiştirmek ancak cisme kuvvet uygulayarak mümkün olur.
Eylemsizlik ilkesinde cisimlerin hareket durumlarını korumaya eğilimli olduklarını öğrenmiştik. Bir cisim duruyorsa durmaya devam etmeye, sabit hızla hareket ediyorsa hızını değiştirmeden hareket etmeye meyillidir. Ama cisimlerin hareket durumları değiştirilebilir. Cisme kuvvet uygularsak hareket durumunu değiştirebiliriz. Örneğin, duran bir cismi itersek hareket etmeye başlamasını sağlayabiliriz. Sabit hızla giden bir cisme gittiği yönde kuvvet uygularsak hızını artırmasını sağlayabiliriz. Aynı cisme hareket yönünün tersinde bir kuvvet uygularsak hızını azaltıp yavaşlatabiliriz. Eğer hareket yönüne dik bir kuvvet uygularsak, hızlandırıp yavaşlatamasak bile yönünü değiştirebiliriz.
Kuvvet ve hareket üzerindeki ilişkiyi tersinden de düşünebiliriz. Eğer bir cismin hareket durumu değişiyorsa üzerine mutlaka bir kuvvet uygulanıyordur. Bir araba duruyorken kendi kendine hareket etmeye başlamaz. Eğer araba hareket etmeye başladıysa üzerinde bir kuvvet uygulanmıştır. Bir araba hızlanıyorsa, yavaşlıyorsa ya da yön değiştiriyorsa, mutlaka hareketindeki bu değişime neden olan bir net kuvvet üzerine uygulanıyor demektir.
Kuvvet ve ivme arasındaki ilişki
Bir cismin üzerine kuvvet uygulanırsa cismin hareket durumuna ne olur? Hatırlarsak, cisimlerin hareket etmeleri için üzerlerine kuvvet uygulanması gerekmiyordu. Sabit hızla düz bir doğru üzerinde hareket eden bir cismin üzerindeki net kuvvet sıfırdır. Ama cisimlerin hareket durumlarını değiştirmek için mutlaka kuvvet uygulanması gerekir. Hareketin sebebi kuvvet değildir, ama hareketin değişmesinin sebebi kuvvettir.
Hareketin değişmesi ne anlama gelir? Bir cismin hareketi üç şekilde değişebilir: (a) Cisim hızlanabilir (b) yavaşlayabilir ve (c) cismin hareket yönü değişebilir. Bu üç durumda da cismin hızının değişmesi söz konusudur. Hızın zamana göre değişmesine ivme dendiğini öğrenmiştik. Öyleyse kuvvetin hareketle olan ilişkisini, kuvvetin ivmeyle olan ilişkisi olarak düşünebiliriz.
Bir cismin hızında büyük bir değişiklik yapabilmek için cisme büyük bir kuvvet uygulamak gerekir. Örneğin, duran bir arabayı 100km/sa hıza çıkarmak için gereken kuvvet, aynı arabayı aynı sürede 50 km/sa hıza çıkarmak için gereken kuvvetin iki katıdır.
Kuvvetin cisimlerin ivmesiyle (hızlarını değiştirmesiyle) olan ilişkisi doğru orantıdır. Bir başka deyişle kuvvet arttıkça ivme artar; kuvvet azaldıkça ivme azalır.
Kuvvet ve kütle arasındaki ilişki
Eylemsizlik ilkesinde cisimlerin hareket durumlarını korumaya eğilimli olduğunu öğrenmiştik. Eylemsizlik ilkesinde eksik kalan bir nokta kütleyle hareketin ilişkisiydi. Aslında eylemsizlik ilkesi hareket ve cisimlerin kütlesiyle ilgili doğrudan bir bilgi içermez. Ama cisimlerin eylemsizliklerini yani hareket durumlarını koruma yatkınlıkları kütleriyle ilişkilidir. Bir cismin kütlesi ne kadar büyükse o cismin hareket durumunu bozmak o kadar zordur.
Tüm cisimlerin hareket durumlarını değiştirebilmek için üzerilerine kuvvet uygulamak gerekir. Ama acaba aynı kuvveti farklı kütleli cisimlere uygularsak hareket durumları nasıl değişir? Bunu bir örnekle açıklayalım. Bir araba bir de kamyon düşünelim. Her ikisi de duruyorken aynı kuvveti uygulayarak arabayı mı, yoksa kamyonu mu harekete geçirmek daha zordur? Elbette kamyonu! Peki, fren yapsalar, araba mı daha zor durur yoksa kamyon mu? Tabii ki kamyon! Bu gözlem bize ne anlatır? Cisimlerin hareketlerini değiştirmek kütleleri arttıkça daha zor hale gelir. Herhangi bir cismin hareket durumunu değiştirmenin cisme kuvvet uygulayarak olabileceğini bildiğimize göre, kuvvetle kütle arasında bir ilişkinin de olduğu çıkarımını yapabiliriz. Bunun anlamı bir cismin hareketini değiştirmek için uygulanan kuvvetin kütleyle doğru orantılı olduğudur.
Newton’un ikinci Hareket Yasası
Kuvvetin ivme ve kütleyle olan ilişkisini birleştirirsek, şöyle bir matematiksel modele ulaşırız:
F = ma
Burada F kuvveti, m kütleyi, a ivmeyi gösterir. Bu matematiksel model, kuvvetin kütleyle ve ivmeyle doğru orantılı olduğunu anlatır. Ayrıca herhangi bir hareket değişiminin nedeninin kuvvet olduğunu söyler. Bir cisme kuvvet uygulanmasının sonucu cismin ivmelenmesidir.
Kuvvet, kütle ve ivme arasındaki bu ilişkiye Newton’un ikinci hareket yasası denir. Newton’un bilime bu katkısı modern bilimi başlatan, teknolojinin gelişimini tetikleyen dev bir başarıdır. Newton’a kadar hareket anlaşılması mümkün olmayan kutsal bir olay olarak düşünülüyordu. Newton’un hareketin sırrını çözmesi, matematiği kullanarak doğayı anlamanın da önünü açtı. Bir anlamda Newton fizik bilimini başlattı diyebiliriz.
Bir olayı olmadan önce bilmek, öngörebilmek bize inanılmaz bir güç sağlar. Bilime bu denli değer vermemizin belki de en önemli nedeni bu öngörü gücüdür. Newton’un hareketi öngörebilmesi, bunun başka doğal olaylar için de mümkün olduğu fikrinin yayılmasını sağladı.
Kuvvet ve ivme ilişkisi: Sanal Deney
Newton’un ikinci hareket yasası acaba doğru mu diye merak edersek, kuvvet ile ivme arasındaki ilişkiyi araştırmak için bir sanal deney yapabiliriz. Bu deneyin videosunu aşağıda izleyebilirsiniz. Videodaki Kuvvet ve Hareket PHET simülasyonunu kullanarak deneyi siz de yapabilirsiniz.
Bir cismin üzerine kuvvet uygulanırsa cismin hızının değiştiğini öğrenmiştik. Bir cismin üzerine kuvvet uygulandığı zaman ivmelendiğini yani hızlandığını ya da yavaşladığını gördük. Ama kuvvetle ivme arasındaki ilişki tam olarak nasıldır? Kuvvet arttıkça ivme nasıl değişir? Bu soruya cevap bulmak için Kuvvet ve Hareket: Temel İlkeler simülasyonunu kullanarak bir deney yapabiliriz.
Deneyin Tasarımı
Bu deneyde, her deneyde olduğu gibi, önce değişkenlerimizi belirlemeliyiz. Bizim değiştirdiğimiz değişken (bağımsız değişken) kuvvet olacak. Bağımsız değişkenin değişmesine bağlı olarak değişen (bağımlı değişken) de ivme olmalı. Kontrol ettiğimiz değişkenlerin biri, yani her denememizde sabit tuttuğumuz değişken kütle olacak. Bir başka kontrol değişkenimiz de sürtünme kuvveti olacak. Bu simülasyonun Hareket sekmesinde çalışacağımız için zaten sürtünme kuvvetinin değeri hep sıfır olacak.
| Bağımsız değişken (biz neyi değiştiriyoruz) | Kuvvet |
| Bağımlı değişken (bağımsız değişkenin değişimine bağlı olarak ne değişiyor) | İvme |
| Kontrol değişkeni (neyi sabit tutuyoruz) | Kütle, sürtünme kuvveti |
Ama ivmeyi nasıl ölçebiliriz? Bunun bir yolu hız değişiminin süresini ölçmek olabilir. Örneğin, cismin hızının sıfırdan en yüksek değerine ulaşana kadar geçen süreyi ölçebiliriz. Bu simülasyonun en yüksek hız değeri 40 m/s. Başlangıçta cismimiz dururken (hızı sıfırken) kuvvet uyguladığımızda hızının ne kadar sürede 40 m/s değerine ulaştığını bir kronometre ile ölçebiliriz.
Veri toplama
Artık “kuvvet ile ivmenin ilişkisi nasıldır” sorusunu araştırmak için veri toplamaya hazırız. Veri toplarken hep aynı kütleyi kullanacağız. Veri toplamaya bağımsız değişkenimizi, yani kuvveti değiştirerek başlayacağız. Önce 100 N, sonra sırasıyla 200 N, 300 N, 400 N ve 500 N değerlerinde kuvvet uygulayacağız. Her uyguladığımız kuvvet değeri için bağımsız değişkenimizi, yani süreyi ölçeceğiz. Her kuvvet değeri için süreyi ölçtükten sonra ivmenin değerini hesaplayabiliriz. Topladığımız veriyi (yani kuvvet ve süre değerlerini) kaydetmemiz gerekli. Bunun için şöyle bir tablo kullanabiliriz. Bu tabloda uygulayacağımız farklı kuvvet değerlerini ve hız değişimi miktarını önceden yazabiliriz. Hız değişimi miktarı (Δv) cismin 0 m/s hızdan (cisim duruyorken) 40 m/s hıza (cismin en yüksek hızına) ulaştığında 40 m/s olduğunu biliyoruz. İvmeyi doğrudan ölçemediğimiz için süreyi ölçüp ivmeyi hesaplayacak şekilde deneyi planladık.
| F (N) | t (s) | Δv (m/s) | a (m/s2) |
|---|---|---|---|
| 100 | 40 | ||
| 200 | 40 | ||
| 300 | 40 | ||
| 400 | 40 | ||
| 500 | 40 |
Veri analizi
Verimizi topladığımıza göre şimdi elimizdeki veriden neler öğrenebiliriz aşaması geliyor. İlk yapmamız gereken verimizin tamamını gösteren tabloya bakmak.
| F (N) | t (s) | Δv (m/s) | a (m/s2) |
|---|---|---|---|
| 100 | 20,38 | 40 | 1,96 |
| 200 | 10,18 | 40 | 3,93 |
| 300 | 6,84 | 40 | 5,85 |
| 400 | 5,06 | 40 | 7,91 |
| 500 | 4,04 | 40 | 9,9 |
Tabloya dikkatlice bakarsak kuvvet arttıkça ivmenin de arttığını görebiliriz. Ama zaten deneye başlarken bunu biliyorduk. Bizim asıl merak ettiğimiz tam olarak kuvvete göre ivmenin nasıl değiştiği. Yani aslında bir matematiksel model (ya da denklem, formül) çıkarabilmeyi istiyoruz. Bunun için verimizi başka türlü görselleştirmeyi deneyebiliriz. En sık kullanılan veri görselleştirme yolu grafik çizmektir. Öyleyse biz de kuvvet ve ivme grafiğini çizebiliriz.
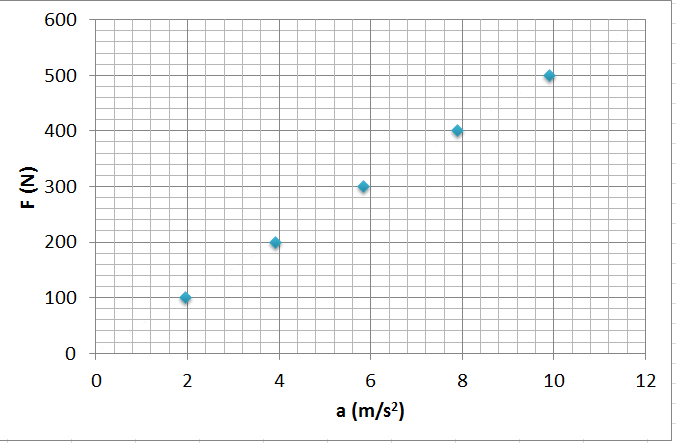
Bu grafikten kuvvet ve ivmenin değerlerini görebiliyoruz. Ama elimizde yalnızca 5 nokta var. Biz tüm noktalar için geçerli olacak bir matematiksel ilişki arıyoruz. Noktalara dikkat ederseniz bir doğrunun üstünde duruyor gibi göründüklerini fark edebilirsiniz. Cetvelle bir çizgi çizip noktalarımızı birleştirmeyi denesek nasıl görünür acaba?
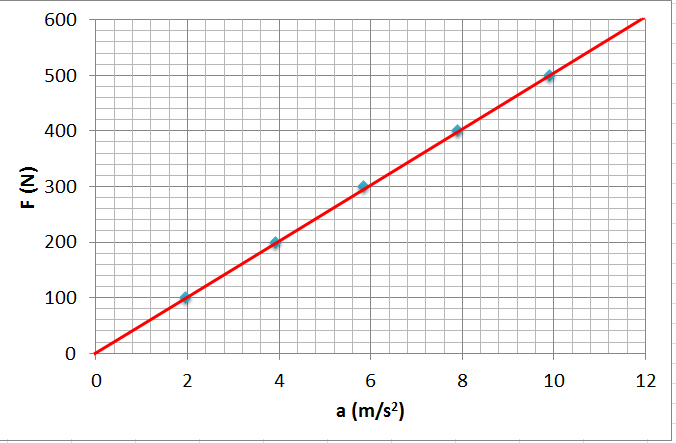
Bu grafikte artık bizim topladığımız 5 veri bir doğrunun üstündeki noktalar haline geldi. Eğer çizdiğimiz doğrunun matematiksel ifadesini bulabilirsek, sorumuza cevap vermiş oluruz. Sorumuz kuvvet ve ivme arasındaki ilişki tam olarak nasıldır olduğunu hatırlayalım. Tam olarak demekle matematiksel bir ilişki (model, denklem ya da formül) aradığımızı da hatırlayalım. Bundan sonrası bir doğrunun denklemini matematiksel olarak yazabilmekte.
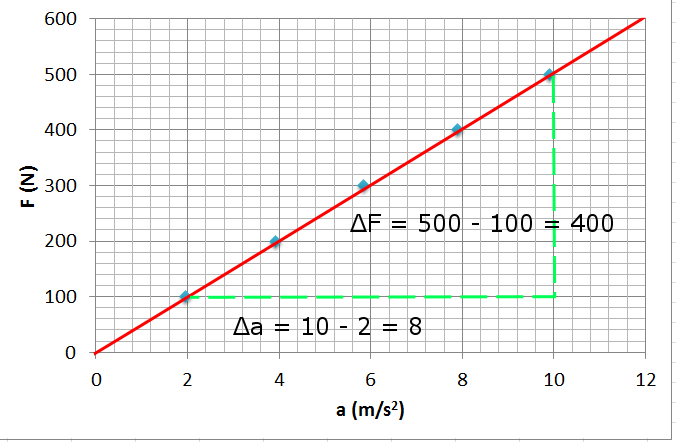
Bir doğrunun denkleminin y = mx + b biçiminde olduğunu biliyoruz. Bu grafikte doğrumuz ekseni (0,0) noktasında kestiği için, doğrunun denklemi y = mx haline geliyor, m katsayısı doğrunun eğimini gösteriyor. Eğimi bulmak için grafiğin üzerinde bir dik üçgen çizebiliriz. Çizdiğimiz dik üçgenin karşı kenarı bölü komşu kenarı bize eğimi verir.
Böylece eğimin ΔF/Δa olduğunu, değerinin de:
m = (500 – 100) / (10 – 2)
m= 400/8 = 50 olduğunu bulabiliriz.
Dikkat ederseniz eğimimizi 50 bulduk, bu bizim kullandığımız cismin kütlesine eşit, yani 50kg.
Bu durumda bizim doğrumuz F = 50a haline geliyor. Bunun anlamı kuvvet ile kütlenin doğru orantılı olması, yani bir doğrunun denklemi şeklinde yazılabilmesi. İlişkiyi daha genel yazarsak F = ma olduğunu görüyoruz.
Sonuç
Kuvvet ile ivme arasındaki ilişki tam olarak nasıldır?
Kuvvet ile ivme doğru orantılıdır (F α a).
Kuvvet = kütle x ivme (F = ma)
Aynı kütleye uygulanan kuvvet değişirse, kütlenin ivmesi de değişir. Kuvvet arttıkça ivme de artar; kuvvet azalırsa ivme de azalır.
Bir kütleye daha çok kuvvet uyguladıkça, hızı daha çabuk değişir.
Kütle ve ivme ilişkisi: Sanal Deney
Newton’un ikinci hareket yasası için kütle ile ivme arasındaki ilişkiyi araştırmak için bir sanal deney yapabiliriz. Bu deneyin videosunu aşağıda izleyebilirsiniz.
Bir cismin üzerine kuvvet uygulandığında cismin hızı artar ya da azalır, yani cisim ivmelenir. Ama Kütle ile ivme arasındaki ilişki tam olarak nasıldır? Acaba aynı kuvvet farklı kütlelere uygulanırsa ivmeye ne olur? Aynı kuvvetin etkisi altında kütle artarsa ivme nasıl değişir? Bu soruya cevap bulmak için Kuvvet ve Hareket: Temel İlkeler simülasyonunu kullanarak bir deney yapabiliriz.
Deney tasarımı
Deneyimizi tasarlamaya başlarken ilk işimiz değişkenleri belirlemek olacak. Bağımsız değişen (bizim değiştirdiğimiz değişken) kütle olacak. Bizim değiştirdiğimiz bağımsız değişkenin değişmesine bağlı olarak değişen (bağımlı) değişken de ivme olmalı. Kontrol ettiğimiz değişken ise uyguladığımız kuvvet olacak.
| Bağımsız değişken (biz neyi değiştiriyoruz) | Kütle |
| Bağımlı değişken (bağımsız değişkenin değişimine bağlı olarak ne değişiyor) | İvme |
| Kontrol değişkeni (neyi sabit tutuyoruz) | Kuvvet |
Peki, ivmeyi nasıl ölçebiliriz? Belki, hız değişiminin kaç saniye sürdüğünü ölçebiliriz. Örneğin, cismin hızının sıfırdan en yüksek değerine ulaşana kadar geçen süreyi ölçebiliriz. Bu simülasyondaki en yüksek hız değeri 40m/s. Başlangıçta hız sıfırken (cisim dururken) kuvvet uyguladığımızda hızının ne kadar sürede 40m/s değerine ulaştığını bir kronometre ile ölçebiliriz.
Veri toplama
Artık “kütle ile ivmenin ilişkisi nasıldır” sorusunu araştırmak için veri toplamaya hazırız. Veri toplarken hep aynı kuvveti kullanacağız. Çünkü deneyimizin adil olmasını istiyoruz. Eğer farklı kuvvetler uygularsak, kütleyle ivmenin ilişkisine bir de kuvveti karıştırmış oluruz. İşte bu yüzden kuvveti kontrol ediyoruz, yani sabit tutuyoruz. Aslında herhangi bir kuvvet değerini kullanabiliriz. Biz bu deneyde F = 500 N değerinde kuvvet uygulamayı seçtik.
Veri toplamaya bağımsız değişkenimizi, yani kütleyi değiştirerek başlayacağız. Önce 40kg, sonra sırasıyla 50 kg, 80 kg, 100 kg, 150 kg, 200 kg, 250 kg ve 300 kg değerlerindeki kütleleri deneyeceğiz. Denediğimiz her kütle değeri için bağımsız değişkenimizi, yani süreyi ölçeceğiz. Her kütle değeri için süreyi ölçtükten sonra ivmenin değerini hesaplayabiliriz. Topladığımız veriyi (yani kütle ve süre değerlerini) kaydetmemiz gerekli. Bunun için şöyle bir tablo kullanabiliriz. Bu tabloda deneyeceğimiz farklı kütle değerlerini ve hız değişimi miktarını önceden yazabiliriz. Hız değişimi miktarının (Δv) 40 m/s olduğunu biliyoruz. Çünkü cismin 0 m/s hızdan (cisim duruyorken) harekete başlayıp 40 m/s hıza (cismin en yüksek hızına) ulaştığını biliyoruz. İvmeyi doğrudan ölçemediğimiz için süreyi ölçüp ivmeyi hesaplayacak şekilde deneyi planladık.
Veri analizi
Verimizi topladığımıza göre şimdi elimizdeki veriden neler öğrenebiliriz aşaması geliyor. İlk yapmamız gereken verimizin tamamını gösteren tabloya bakmak.
| m (kg) | t (s) | Δv (m/s) | a (m/s2) | 1/m (1/kg) |
| 40 | 3,28 | 40 | 12,20 | 0,025 |
| 50 | 4,08 | 40 | 9,80 | 0,02 |
| 80 | 6,52 | 40 | 6,13 | 0,0125 |
| 100 | 8,2 | 40 | 4,88 | 0,01 |
| 150 | 12,2 | 40 | 3,28 | 0,0067 |
| 200 | 16,4 | 40 | 2,44 | 0,005 |
| 250 | 20,4 | 40 | 1,96 | 0,004 |
| 300 | 24,68 | 40 | 1,62 | 0,0033 |
Tablodaki tüm değerler 500 N kuvvet uygulanan durum için kaydettiğimiz veriler. Aslında biz kütleyi değiştirdik ve süreyi ölçtük. Ama ivme değerlerini de hız değişimi miktarını bildiğimiz için (40 m/s) hesaplayıp tabloya yazabildik. Tablonun son sütununa 1/m yani kütlenin matematiksel tersinin değerlerini de ekledik. Daha sonra veriden anlam çıkarmakta işimize yarayabilir bu sütün.
Tabloya dikkatlice bakarsak kütle arttıkça ivmenin azaldığını görebiliriz. Ama zaten deneye başlarken bunu biliyorduk. Bizim asıl merak ettiğimiz tam olarak kütleye göre ivmenin nasıl değiştiği. Yani aslında bir matematiksel model (ya da denklem, formül) çıkarabilmeyi istiyoruz. Bunun için verimizi başka türlü görselleştirmeyi deneyebiliriz. En sık kullanılan veri görselleştirme yolu grafik çizmektir. Öyleyse biz de kuvvet ve ivme grafiğini çizebiliriz.
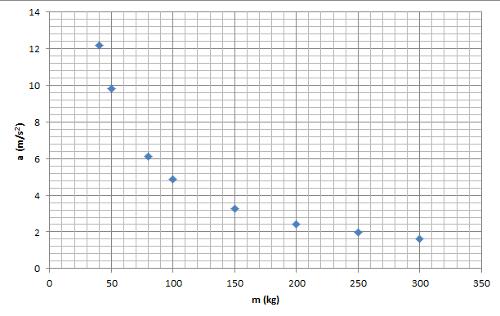
Bu grafikten kütle ve ivmenin değerlerini görebiliyoruz. Ama elimizde yalnızca 8 nokta var. Biz tüm noktalar için geçerli olacak bir matematiksel ilişki arıyoruz. Noktalara dikkat ederseniz azalan bir eğrinin üstünde duruyor gibi göründüklerini fark edebilirsiniz. Bir eğri çizip noktalarımızı birleştirmeyi denesek nasıl görünür acaba?
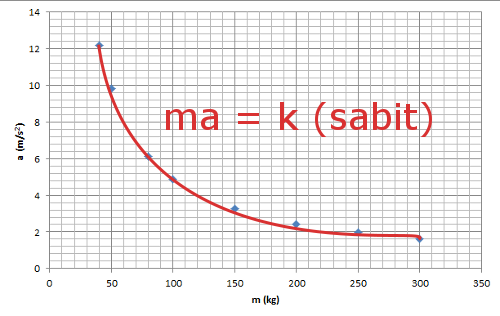
Bu grafikte artık bizim topladığımız 8 veri bir eğrinin üstündeki noktalar haline geldi. Eğer çizdiğimiz eğrinin matematiksel ifadesini bulabilirsek, sorumuza cevap vermiş oluruz. Sorumuz kütle ve ivme arasındaki ilişki tam olarak nasıldır olduğunu hatırlayalım. Tam olarak demekle matematiksel bir ilişki (model, denklem ya da formül) aradığımızı da hatırlayalım. Bundan sonrası bu eğrinin denklemini matematiksel olarak yazabilmekte. Bu eğri bir ters orantı eğrisine benziyor. Yani değişkenlerin çarpımı sabit bir sayıyı veriyor: ma=k
Eğrinin denklemini çıkarmamız biraz zor görünüyor. Acaba başka ne yapabiliriz? Veri analizinde sıklıkla kullandığımız bir numarayı deneyebiliriz: Değişkenlerin birinin matematiksel tersini almayı deneyebiliriz. (Tablo’daki son sütunda 1/m değerlerini aslında bu işi yapabilmek için hesaplamıştık.)
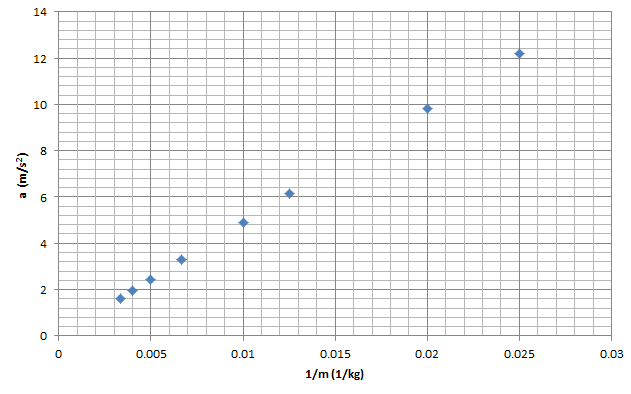
İvmenin (a) kütlenin matematiksel tersine (1/m) göre grafiğine bakınca doğrusal bir biçim görüyoruz. Ama elimizde yalnızca 8 nokta var. Biz tüm noktalar için geçerli olacak bir matematiksel ilişki arıyoruz. Noktalara dikkat ederseniz bir doğrunun üstünde duruyor gibi göründüklerini fark edebilirsiniz. Cetvelle bir çizgi çizip noktalarımızı birleştirmeyi denesek nasıl görünür acaba?
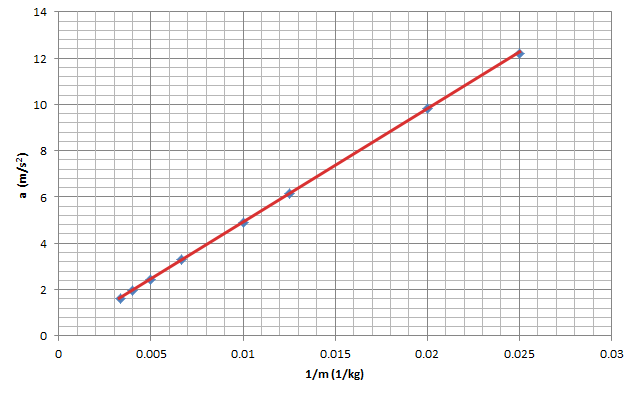
Bu grafikte artık bizim topladığımız 8 veri bir doğrunun üstündeki noktalar haline geldi. Eğer çizdiğimiz doğrunun matematiksel ifadesini bulabilirsek, sorumuza cevap vermiş oluruz. Sorumuz kütle ve ivme arasındaki ilişki tam olarak nasıldır olduğunu hatırlayalım. Tam olarak demekle matematiksel bir ilişki (model, denklem ya da formül) aradığımızı da hatırlayalım. Bundan sonrası bir doğrunun denklemini matematiksel olarak yazabilmekte.
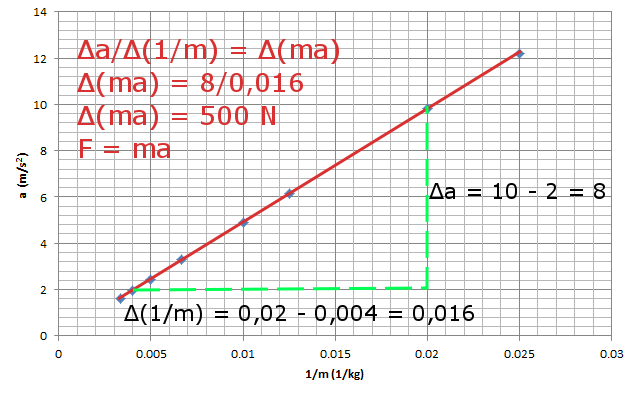
Bir doğrunun denkleminin y = mx + b biçiminde olduğunu biliyoruz. Bu grafikte doğrumuz ekseni (0,0) noktasında kestiği için, doğrunun denklemi y = mx haline geliyor, m katsayısı doğrunun eğimini gösteriyor. Eğimi bulmak için grafiğin üzerinde bir dik üçgen çizebiliriz. Çizdiğimiz dik üçgenin karşı kenarı bölü komşu kenarı bize eğimi verir.
Böylece eğimin Δa/Δ(1/m) olduğunu bu ifadeyi düzenlersek eğimin Δ(ma) olduğunu görebiliriz. Eğimin değerinin de:
Eğim = (10 – 2) / (0,02 – 0,004)
Eğim = 8/0,016 = 500 olduğunu bulabiliriz.
Dikkat ederseniz eğimimizi 500 bulduk, bu bizim cisme uyguladığımız kuvvete eşit, yani 500 N.
Bu durumda bizim doğrumuz 500 = ma haline geliyor. Bunun anlamı kütle ile ivmenin ters orantılı olması, yani biri arttıkça diğerinin azalması. İlişkiyi daha genel yazarsak F = ma olduğunu görüyoruz.
Sonuç
Kütle ile ivme arasındaki ilişki tam olarak nasıldır?
Kütle ile ivme ters orantılıdır (F 1/α a).
Kuvvet = kütle x ivme (F = ma)
Aynı kuvvet farklı kütlelere uygulanırsa ivme değişir. Kuvvet sabitken, kütleyi artırırsanız ivme azalır; kütleyi azaltırsanız ivme artar.
Bunun anlamı aynı kuvveti uygulayarak büyük bir kütlenin hareket durumunu değiştirmenin, küçük bir kütleye göre daha zor olduğudur.
F=ma ile ilgili Fizik dersi Kazanımları
9.3.3.2. Kuvvet, ivme ve kütle kavramları arasındaki ilişkiyi açıklar.
- Net kuvvet, ivme ve kütle arasındaki matematiksel model verilir.
- Serbest cisim diyagramı üzerinde cisme etki eden kuvvetler gösterilir. Net kuvvetin büyüklüğü hesaplanarak yönü gösterilir.
- Hesaplamalarda yatay düzlemde tek kütle ile sınırlı kalınır. Bileşenlere ayırma hesaplamalarına girilmez.
- Yer çekimi ivmesi açıklanarak ağırlık hesaplamaları yapılır.
Çok teşekkür ederim . Çok çok yardımcı, mantığı kavratıcı olmuş .
ALLAHIM İYİKİ BU SİTEYİ BULMUŞUM :DDDDDDD
Çok çok güzel ve anlaşılır açıklanmış.