Hacim nedir nasıl ölçülür? Tanımı ve birim dönüşümleri

Hacim nedir sorusunun cevabı bir cismin uzayda yani boşlukta kapladığı yerdir. Uzay üç boyutludur bu yüzden hacim her zaman üç boyutludur. V simgesiyle gösterilir. Katıların, sıvıların ve gazların; genel olarak maddenin ortak özelliğidir. Belirli bir basınçta ve sıcaklıkta katıların ve sıvıların belirli bir sabit hacmi vardır, gazlar ise içine konuldukları kabın hacmini alırlar, hacimleri değişkendir.

Hacim birimleri ve birim dönüşümleri

Hacim skalerdir ve türetilmiş bir niceliktir. Hacmin birimi metreküptür (m³). Bir metreküp, ayrıtları 1 m olan bir kübün hacmine eşittir. Metreküp cinsinden birimler biner biner azalır ve artar. Aşağıdaki tablo bunu gösteriyor:

Birim	m3 karşılığı
metreküp (m3)	1
desimetreküp (dm3)	10-3
santimetreküp (cm3)	10-6
milimetreküp (mm3)	10-9

Ayrıca özellikle sıvıların hacmini ölçerken litre (L) sıklıkla hacim birimi olarak kullanılır.

1 litre = 1 dm³ = 1000 cm³ = 10^-3 m³

Litre’nin askatları onar onar azalır. Aşağıdaki tabloda bu görülüyor:

Birim	Litre karşılığı
litre (L)	1
desilitre (dL)	10-1
santilitre (cL)	10-2
mililitre (mL)	10-3

Örnek soru – Hacim birim dönüşümü litreden metreküpe

Bir insan ömrü boyunca ortalama 24500 L tükürük salgılar. Salgılanan tükürüğün hacmi (a) kaç m³‘tür (b) kaç cm³‘tür?

Çözüm:

(a) Önce 1 litreyi (L) 1 m³‘e dönüştürelim.

1 L = 10^-3 m³

Şimdi eşitliğin iki tarafını da 24500 ile çarpalım.

24500 L = 24500 x 10^-3 m³

24500 = 24,5 x 10³

Öyleyse derli toplu yazınca:

24500 L = 24,5 x 10³ x 10^-3 m³ = 24,5 m³

(b) Artık elimizde kaç metreküp tükürük olduğunu biliyoruz. Şimdi metreküpü santimetreküpe dönüştürelim.

Öncelikle 1 cm³ = 10^-6 m³ olduğunu üstteki tablodan biliyoruz.

Eşitliğin iki tarafını da 10⁶ ile çarpalım.

10⁶ cm³ = 10⁶ x 10^-6 m³

10⁶ cm³ = 1 m³

Şimdi 24,5 m³‘ü cm³ cinsinden yazalım.

24,5 m³ = 24,5 x 10⁶ cm³

Düzgün Geometrik Cisimlerin Hacimleri nasıl hesaplanır?

Küp

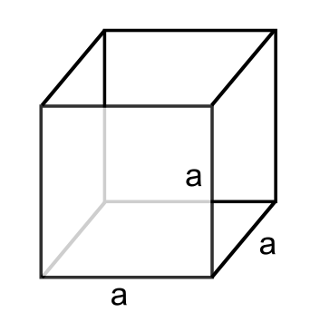
Küpün hacmi bir kenarının üç kez kendisiyle çarpılmasıyla hesaplanır.

V_küp = a x a x a = a³

a küpün her ayrıtının uzunluğudur.

Kare prizma

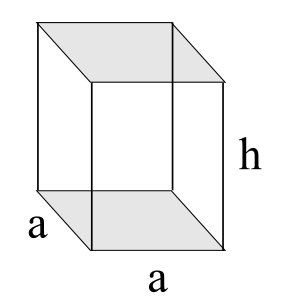
Kare prizmanın hacmi taban alanıyla yüksekliğinin çarpımıyla bulunur. Taban alanı bir karedir.

V_{kare prizma} = a x a x h = a²h

a tabandaki karenin bir kenarının, h yüksekliğin uzunluğudur.

Dikdörtgenler prizması

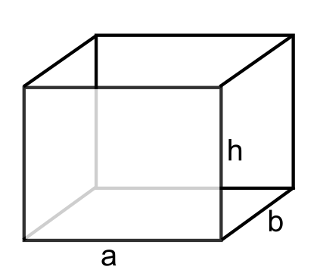
Dikdörtgenler prizmasının hacmi taban alanıyla yüksekliğin çarpımıyla hesaplanır.

V_{dikdörtgenler prizması} = a x b x h = abh

a ve b tabandaki dikdörtgenin kenar uzunlukları, h yüksekliğin uzunluğudur.

Silindir

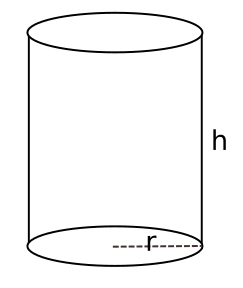
Silindirin hacmi taban alanıyla yüksekliğin çarpımıyla bulunur. Taban alanı dairedir.

V_silindir = πr² x h = πr²h

r tabandaki dairenin yarıçapının, h silindirin yüksekliğinin uzunluğudur.

Küre

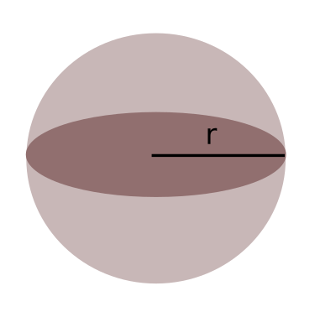
Kürenin hacmi şöyle bulunur:

V_{kure} = \frac{4}{3} \pi r^3

r kürenin yarıçapının uzunluğudur.

Koni

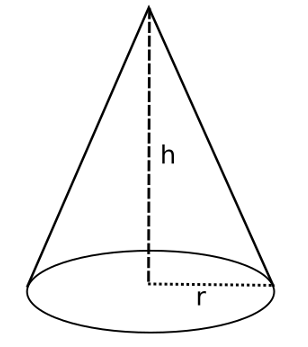
Koninin hacmi şöyle bulunur:

V_{koni} = \frac{1}{3} \pi r^2h

r tabandaki dairenin yarı çapıdır, h koninin yüksekliğidir.

Hacim nasıl ölçülür?

Katıların, sıvıların ve gazların hacimlerini ölçmek için çeşitli yöntemler kullanabiliriz.

Katıların hacmi nasıl ölçülür?

Düzgün geometrik şekilli katıların hacmi hesaplanabilir, ama hesaplamakla ölçmek aynı şey değildir.

Dereceli Silindir

Düzgün şekli olan ve olmayan tüm katı cisimlerin hacmini dereceli silindirin içine konulmuş bir sıvının silindirin içinde yükselme miktarından bulabiliriz. Su, içine cisim girince yükselir çünkü cismin hacmi kadar yer değiştirir. Ancak bu sadece sıvıda batan cisimler için geçerlidir. Örneğin, tahta bir bloğun hacmini dereceli silindirin içinde su kullanarak ölçemeyiz.

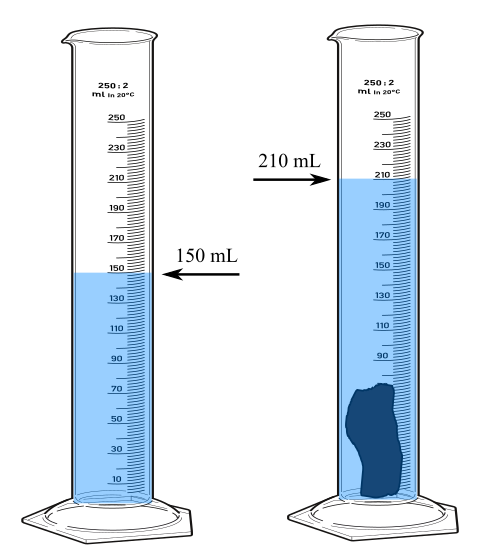
1. Önce dereceli silindirin içine su koymalısınız. Ölçmek istediğiniz cismin hacminden daha fazla su koymalısınız, yoksa ölçemezsiniz.
2. Ölçmek istediğiniz cisim suda yüzmemeli, tamamen batmalı, yoksa hacmini eksik ölçersiniz.
3. Önce sadece su dolu silindirin suyun yüzeyindeki işaretinin kaç mL olduğunu okuyun ve kaydedin.
4. Sonra cismi dereceli silindirin içine dikkatlice bırakın. Çok hızlı atarsanız su silindirin dışına sıçrayabilir, ölçümünüzde hata olur.
5. Şimdi içinde cisim ve su olan silindirdeki suyun yüzeyinin denk geldiği çizgiyi okuyun ve kaydedin.
6. Artık cismin hacmini bulabilirsiniz: 5. adımdaki hacim değerinden 3. adımdaki hacim değerini çıkarın.

Resimdeki örnekte dereceli silindirin içinde yalnız su varken hacim değeri 150 mL, cismi attıktan sonra 210 mL olmuş. Öylese bu cismin hacmi 210 mL – 150 mL = 60 mL.

Taşırma Kabı

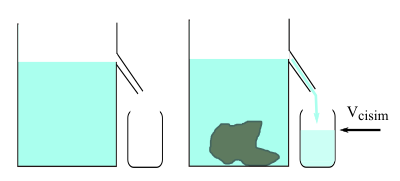
Taşırma kabı (Evreka kabı da denir) üstünde bir boru olan kavanoz gibi bir şeydir. Borunun seviyesine kadar su doldurursunuz ve borunun altına da bir başka boş kavanoz ya da beher yerleştirirsiniz. Hacmini ölçmek istediğiniz şeyi taşırma kabının içine bırakırsınız, yine dışarı su sıçratmamaya dikkat etmeniz gerekir. Sonra içine cisim girince taşırma kabındaki su yükselir (taşar) ve borudan akmaya başlar. Borudan su akışı kesilinceye kadar beklersiniz, bitince ikinci kavanozda biriken suyun hacmini ölçersiniz ve katı cismin hacmini ölçmüş olursunuz.

Sıvıların hacmi nasıl ölçülür?

Sıvıların hacmi dereceli kaplarla ölçülür, dereceli silindir örneğinde bunu gördük. Aşağıda bir kaç dereceli kap (bunlara beher de denir) resmi görülüyor.

Birbirine karışmayan sıvılarda sıvıların ayrı ayrı hacimlerini ölçeriz, toplam hacim ikisinin toplamı olur. Birbirine karışan sıvılarda hacim ayrı ayrı ölçüldüğünden biraz daha az olur.

Gazların hacmi nasıl ölçülür?

Gazların hacmi sıcaklığa ve basınca göre değişir. Bir gazın hacminden bahsederken daima hangi sıcaklıkta ve hangi basınçta ölçümün yapıldığı söylenmek zorundadır. Aşağıdaki resimde kimyasal tepkime sonucu ortaya çıkan bir gaz borudan geçerek içi sıvı dolu bir dereceli silindiri dolduruyor. Sıvı gazla yer değiştiriyor. Böylece dereceli silindirde biriken gazın hacmini okumamız mümkün oluyor.

Hacim ile ilgili Fizik dersi Kazanımları

9.2.1.1. Özkütleyi, kütle ve hacimle ilişkilendirerek açıklar.

• Düzgün geometrik şekilli cisimlerden küp, dikdörtgenler prizması, silindir, küre ve şekli düzgün olmayan cisimler için hacim hesaplamaları yapılır. Kum-su problemlerine girilmez.