Düzgün çembersel hareket (veya dairesel hareket) için temel kavramlar olan periyot, frekans, açısal hız, merkezcil ivme ve merkezcil kuvveti öğrenmiştik. Şimdi yatay ve düşey düzlemlerde çembersel hareket yapan cisimlerin hareketini analiz edeceğiz, yani parçalarına ayırıp inceleyeceğiz. Çembersel hareket yapan cisimlerin önce hareketli resimlerini göreceğiz, sonra serbest cisim diyagramlarını çizip üzerlerindeki kuvvetleri göstereceğiz. Yatay düzlemde düzgün çembersel hareketi gerçekleştirmenin kolay olduğunu, ama düşey düzlemde çembersel hareket için düzgünlüğü sağlamanın (çizgisel süratin sabit kalmasının) o kadar kolay olmadığını keşfedeceğiz.
Yatay düzlemde düzgün çembersel hareket ve serbest cisim diyagramı
Yatay düzlemde düzgün çembersel hareket yapan bir cisim yer yüzündeyse bir masanın ya da zeminin üstünde dönüyordur. Aşağıdaki resimde bir odanın zeminine çember şeklinde bir hulahop yerleştirilmiş, içinde de bir tenis topu çemberin iç kenarına değecek şekilde fırlatılmış. Tenis topunun saat yönünün tersine doğru döndüğünü görüyoruz. (Açısal hız vektörünün yönünü bulabilir misiniz?)

Bu tenis topunu hareketinin bir anında durduralım ve üzerindeki kuvvetleri gösterelim. (Yere yukarıdan bakıyoruz, kamera yukarıdan çekiyor yani.) Aşağıdaki resim, hareketin bir anında durdurulmuş bir karesini gösteriyor. Bu topun dönmesinin nedeni hulahopun kenarlarının topu itip sürekli yönünü değiştirmesi. (Hulahopu bir anda kaldırırsak top nasıl hareket eder?)

Şimdi de aynı hulahopa üstten değil yandan bakalım. Kamerayı hem zemine paralel hem de topa dik bir yere yerleştiriyoruz. Bu kez serbest cisim diyagramını çizeceğiz. Serbest cisim diyagramı çizmek demek cismin üzerindeki kuvvetleri göstermek anlamına geliyor. Aşağıdaki resimde topun üstünde yatay doğrultuda sadece hulahopun çeperinin uyguladığı kuvvet olduğu, düşey doğrultuda ise topun ağırlığı ve zeminin topa uyguladığı normal kuvvetin olduğu görülüyor. (Bu durum için sürtünmeyi ihmal edelim. Ağırlığın kütle ile yer çekimi ivmesinin çarpımı olduğunu da hatırlayalım.) Bu kuvvetlerin bileşkesinin (yani net kuvvetin) yalnızca hulahopun topa uyguladığı yatay kuvvet olduğunu görüyoruz. Çünkü düşeyde aşağı doğru olan topun ağırlığını yukarı doğru olan normal kuvvet dengelemiş.
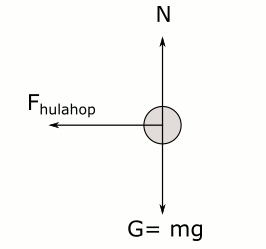
Serbest cisim diyagramında topun dönmesini sağlayan merkezcil kuvvetin kaynağının hulahopun çeperlerinin topu itmesi olduğunu görüyoruz. Eğer top düzgün çembersel hareket yapıyorsa (yani çizgisel sürati sabitse), çembersel yörüngenin her noktasında yukarıdaki serbest cisim diyagramı geçerli. Hulahopun uyguladığı itme kuvvetinin büyüklüğü her noktada aynı.
F_{hulahop}=m\frac{v^2}{r}=m\omega^2rAşağıdaki resimde de bir yoyo ipinin ucundan tutulup bir masanın üstünde çevriliyor. Yoyonun dönmesinin nedeni ipin sürekli onu içeri doğru çekmesi.

Bu yoyonun serbest cisim diyagramı yukarıdaki hulahopun diyagramının tam olarak aynısı olur (yine sürtünmeyi önemsemiyoruz). Tek fark tenis topunu çemberin merkezine iten hulahopun kenarlarıydı, yoyoyu merkezin çemberine çeken ip. Bu durumda ipteki gerilme kuvveti merkezcil kuvveti sağlıyor. Aşağıdaki resimde de yoyonun serbest cisim diyagramı gösteriliyor.
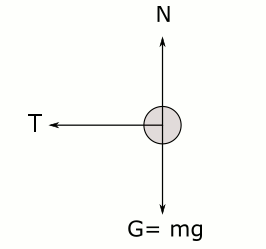
Merkezcil kuvvet olmasa yoyo dönemez, adam ipi bırakırsa yoyo nasıl hareket eder? Eğer cisim düzgün dairesel hareket yapıyorsa ipteki gerilme kuvvetinin büyüklüğü her noktada aynı, yani aşağıdaki serbest cisim diyagramı yörüngenin her noktası için geçerli. (T ipin gerilimini gösteriyor.)
T=m\frac{v^2}{r}=m\omega^2rSon olarak bir de döndürme masası (ya da döndürme tablası DJ’lerin turntable dedikleri de aynı şey) üzerine yerleştirilmiş fanus içinde yanan bir mumun düzgün çembersel hareketini inceleyelim. Aşağıdaki resimde önce mumun tabanına bakacağız. Mum neden dönebiliyor? Çünkü döndürme masasıyla mumun tabanı arasındaki sürtünme kuvveti mumu içeri doğru çekiyor (yoksa itiyor mu? Fark eder mi?) Mumun açısal hızının yönünü bulabilir misiniz?

Mumun tabanının serbest cisim diyagramı hulahopun içindeki tenis topununkiyle ve ipin ucundaki yoyoyla tam olarak aynı. Tek fark merkezcil kuvvetin kaynağının bu kez mumun tabanı ile masa arasındaki sürtünme kuvveti olması. Hareket düzgün çembersel ise serbest cisim diyagramı her noktada aynı ve sürtünme kuvvetinin büyüklüğü de her noktada aynı.
F_{surtunme}=m\frac{v^2}{r}=m\omega^2rMumun tabanının serbest cisim diyagramı da aşağıdaki gibi çizilebilir. Mumun tabanına bir parçacık gibi davrandığımıza dikkat edin. Peki bu statik sürtünme mi kinetik sürtünme mi?
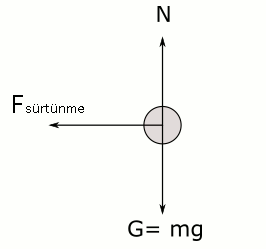
Şimdi de mumun alevine bakalım. Yukarıdaki resimde çok dikkatli bakarsanız mumun alevinin masanın merkezine doğru büküldüğünü görebilirsiniz. Daha iyi görünmesi için bir kareyi dondurup büyüttük. Aşağıdaki gibi görünüyor, mumun alevi masanın yani çembersel yörüngenin merkezine doğru bükülmüş. Ama neden?

Mumun alevinin serbest cisim diyagramını çizersek görebiliriz. Bu bir meydan okuma: Mumun alevinin serbest cisim diyagramını çizebilir misiniz? (Çok iyi sınav sorusu olurdu.) Merkezcil kuvvetin kaynağı ne?
Düşey düzlemde çembersel hareket ve serbest cisim diyagramı
Düşey düzlemde çembersel hareket yapan (dikkat edin düzgün demedim) bir cisimden bahsederken, yeryüzünde olduğunu farz ediyoruz, dolayısıyla yer çekimi kuvvetini de hesaba katmamız gerekiyor.

Yukarıdaki resimde bir adam bir ipin ucuna bağlanmış bir tenis topunu düşey düzlemde çeviriyor.
Topun serbest cisim diyagramını çembersel hareketin yörüngesinin farklı noktalarında çizelim. Aşağıdaki resimde 8 farklı nokta gösteriliyor. İlk beşini açıklayalım, 6., 7. ve 8. konumlardaki serbest cisim diyagramlarını siz çizin. (Simetri işinizi kolaylaştırabilir.)
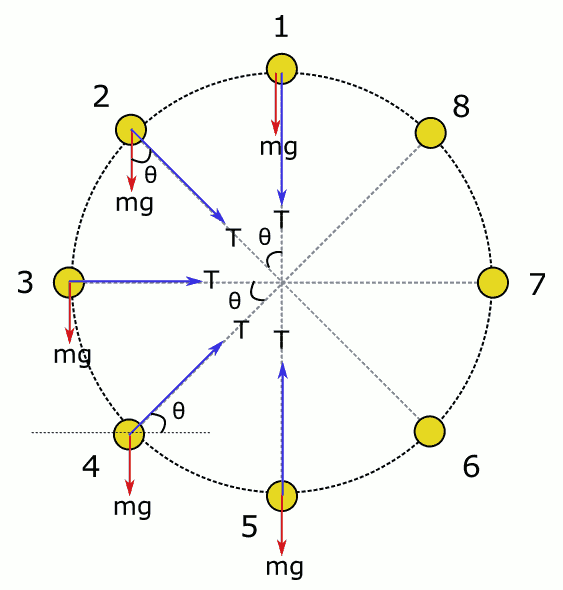
Cismin düzgün çembersel hareket yapabilmesi için merkezcil kuvvetin büyüklüğünün her noktada eşit olması gerekiyor (Neden?) Yörüngenin tüm noktalarında vektörel olarak kuvvetlerin toplamı şöyle olmak zorunda:
\vec{F}_{merkezcil}= m\vec{g}+\vec{T}(1) numaralı konumda top yörüngenin en tepesinde. Buna göre ip gerilimi ile cismin ağırlığının toplamı merkezcil kuvvete eşit. Ayrıca ağırlığın ve ip geriliminin yönleri de aynı olduğu için vektörlerin büyüklükleri için de aynı ilişki geçerli:
F_{merkezcil} = T + mg(5) numaralı konumda ise yalnızca düşey doğrultuda ağırlık ve ip gerilimi var, ikisi zıt yönlü:
F_{merkezcil}=T-mg(1) ve (5) numaralı konumlarda bu cisim düzgün çembersel hareket yapabilir, çünkü cisme uygulanan kuvvet hep çembersel yörüngenin merkezine doğru. Çembere teğet yönde kuvvet yok, Newton’un birinci yasasına göre çembere teğet yönde net kuvvet sıfır olduğu için çizgisel ivme olamaz, çizgisel sürat sabit kalır.
Kolay olanlara önce baktık, şimdi sıra biraz daha karmaşık görünenlerde.
(3) numaralı konumda merkezcil kuvvet yönünde sadece ip gerilmesi var, bu çembersel hareketi açıklıyor. İp cismi çemberin merkezine doğru çekiyor.
F_{merkezcil} = TAma bir sorun var, ağırlık çembere teğet yönde ve dengeleyecek bir kuvvet de yok. Newton’un ikinci yasasına göre bu cisim çembere teğet yönde ivmelenmek zorunda, çünkü dengelenmemiş bir kuvvetin etkisinde. Öyleyse çizgisel sürat de değişmek zorunda. Yani bu cisim (3) numaralı konumda çembersel hareket yapıyor, ama düzgün çembersel hareket yapmıyor.
(2) numaralı konumda topun üstünde aşağı yönlü ağırlığı ve hem aşağı (-y yönünde) hem de sağa (+x eskeni yönünde) doğru bileşenleri olan ip gerilimi var. Vektörleri istediğimiz koordinat sistemine göre bileşenlerine ayırabiliriz. Eğer ağırlığın merkezcil kuvvet doğrultusundaki bileşenini alırsak:
F_{merkezcil} = T + mgcos\theta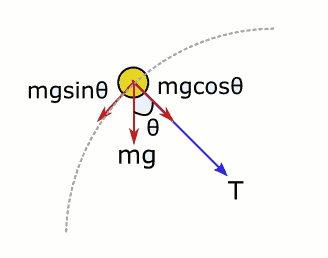
Ağırlığın yarıçap üzerindeki bileşeniyle (mgcosθ) ip geriliminin yönlerinin aynı olduğuna dikkat etmelisiniz. Bu çembersel hareketi açıklıyor, ama ya ağırlığın çembere teğet olan bileşeni ne olacak? Tıpkı (3) numaralı konumda olduğu gibi burada da çizgisel ivme olmak zorunda, yani cisim düzgün çembersel hareket yapmıyor.
(4) numaralı konumda -y yönünde ağırlık, +x ve +y yönünde bileşenleri olan ip gerilmesi var. Yine ağırlığın merkezcil kuvvet yönündeki bileşenini alırsak:
F_{merkezcil} = T - msin \theta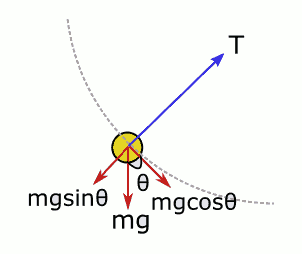
Bu durumda yarıçap üzerindeki bileşeniyle (mgsinθ, neden sin oldu?) ip geriliminin yönlerinin zıt olduğuna dikkat etmelisiniz. Tıpkı (3) ve (4) numaralı konumlarda olduğu gibi ağırlığın çembere teğet olan bileşeni çizgisel ivmeye neden oluyor, düzgün çembersel hareket ortadan kalkıyor. Ama yörünge çember olduğu için hareket hala çembersel hareket.
Bir meydan okuma daha: İpe bağlı düşey çembersel hareket yapan bir cismin düzgün çembersel hareket yapmasını sağlayabilir misiniz? Peki ya ipe bağlı bir cisim değil de bir rayın üzerinde hareket eden bir hız trenine düzgün çembersel hareket yaptırmak mümkün olabilir mi, nasıl? (Test ya da sınav sorularında eğer ray, yol gibi birşey vermemişse ve cisim düzgün çembersel hareket yapıyor demiyorsa, soru da sorun var demektir.)
Son bir meydan okuma. Aşağıdaki videoda bir adam içi su dolu bir kovayı düşey düzlemde çeviriyor. Kova adamın başının üstüne gelmesine rağmen içindeki su dökülüp adamı ıslatmıyor. Bu durumu nasıl açıklarsınız?
Yatay ve düşey düzlemde çembersel hareket ile ilgili kazanımlar
2017 – 12.1.1.3. Düzgün çembersel hareket yapan cisimlerin hareketini analiz eder.
- Yatay ve düşey düzlemde düzgün çembersel hareket yapan cisimlere ait serbest cisim diyagramlarının çizilmesi sağlanır.
Yatay ve düşey düzlemde çembersel hareket ile ilgili MEB ve EBA Testleri
- Çembersel hareket Test 3 (2018)
- Kuvvet ve Hareket Test 13 (2016)
Merhabalar,
Mum alevinin içeri doğru yönelmesinin sebebi, havanın muma uyguladığı sürtünme kuvveti midir? Mum çembersel hareket yaparken havanın sürtünmesinden dolayı merkezcil kuvvet oluşuyor. Bunun sonucunda mum alevi merkeze yöneliyor. Doğru mu düşünüyorum acaba? Birde eylemsizlik sebebiyle olabilir mi acaba diye de düşündüm ama emin değilim.
Son meydan okumada ise kovanın içindeki suyun serbest cisim diyagramını çizmeye çalıştım ancak doğru mu yaptım emin değilim. Kova içindeki tam tepedeyken aşağı doğru mg ve merkezkaç kuvveti uygulanıyor. Suyun kovada kalmasını sağlayan kuvvet nedir anlayamadım. Yani olay gözümde canlansa da fiziksel ve matematiksel olarak ifade edemiyorum. Biraz ipucu iyi olurdu 🙂
İyi çalışmalar
Mum alevi için, rüzgar ne demek onu düşün diye ipucu verebilirim. Eylemsizlikle ne ilgisi olabilir rüzgarın? Rüzgarla mum alevinin ne ilgisi olabilir? Kovanın içindeki su için de, suyun eğik atış yapıyor olma ihtimalini bir değerlendir derim. Serbest cisim diyagramları işine yarayabilir, fotoğraflarını çekip gönderebilirsin de.
Bekliyorum bu konudaki ilerlemeni ve düşüncelerini.
Tekrar merhaba,
https://hizliresim.com/g9m6ZO
Yukarıda linki paylaştım, mum alevine etki eden kuvvetler var. Şöyle düşünüyorum son araştırmalarımdan sonra;
1. Mumun için bulunduğu kaptaki hava tabla dönerken bir merkezcil kuvvete maruz kalıyor ve mum alevinin de merkezcil bir ivme yapmasına sebep oluyor.
2. Mum alevinin kendi ağırlığından dolayı bir mg’si ve bu mg’nin normali var (G ve N) bunlar birbirini dengeliyor.
3. Eğer sadece bu üç kuvvet olsaydı, yani Fmerkezcil, G ve N, mum alevi yatay x ekseni boyunca yönlenmeliydi. Ancak tam yatayda değil, çapraz yönleniyor. Bunun sebebinin de bu kuvvetlere ek olarak havanın kaldırma kuvveti etkisinin olduğunu düşünüyorum. Zaten mumu yakınca alevin yukarı yönelmesi sanırım başka bir şey ile açıklanmaz.
Ekleme ve düzeltmelerinizi bekliyorum.
Suyun dökülmemesi hala tam oturmadı kafamda ama şunu düşündüm, su dolu kova dönerken aslında biz merkezcil kuvveti kovaya uyguluyor. Bu kuvvet sebebiyle kova da suya bir kuvvet uyguluyor. Newton 3.yasası etki-tepkiye göre de suyun merkezcil kuvvetin tersi yönde kovaya bir kuvvet uygulaması gerekir. Mi acaba? Şu an bu aşamadayım 🙂
Teşekkürler ilginize.
Mum alevinin kaldırma kuvvetiyle ilişkisi benim aklıma hiç gelmemişti, ama çok mantıklı. Merkezcil kuvvetin sebebi önemli burada, alevi merkeze doğru büken kuvvetin nedeni ne olabilir? Haklısın bu fanusun içindeki havanın içeriye doğru itilmesiyle ilişkili. Tabla dönerken hava eylemsizlikten dolayı hızının yönünü korumaya meyilli. Ama fanusun çeperlerinin yeri sürekli değişiyor, çünkü dönüyor. Çeperler havaya çarpıp, havayı içeri doğru itiyor. Havayı elinle itince ne olur? Rüzgar değil mi? Bu da aynı şey. Tablanın üstündeki fanus dönmeye devam ettikçe, hep merkeze doğru bir rüzgar oluşuyor. Alev bu nedenle içeri doğru bükülüyor. Daha sonra Coriolis kuvveti diye yine sanal (hayalet) bir kuvvet öğreneceksin eğer fiziği merak etmeye devam edersen. Dünyanın dönmesinden kaynaklanan, kuvvetli rüzgarları oluşturan kuvvet Coriolis kuvveti.
Kovanın içindeki suyu açıklamadan önce eğik atışı anlatmam lazım, daha onu yazamadım. Yazdıktan sonra bunu hatırlat tekrar bakalım.
Serbest cisim diyagramın çok iyi olmuş, tebrikler.
Mum alevinin dönme eksenine bakan kısmı ile dışarı bakan kısmı arasında basınç farkı meydana gelir. Dışarı bakan kısımdaki basınç içeri bakan kısımdaki basınçtan her zaman büyük olur. Bu fark mum alevini merkeze doğru yönlendirir. Alevin ısısıyla çevresindeki havanın yoğunluğu azalacağı için mum Alevi yükselmek isteyecektir. Burada bir yandan basınç farkı diğer yandan özkütlesi azalan havanın yukarı çıkmak istemesi mum alevinin çapraz (yatay ile düşey arasında) kalmasına neden olur.
Mum alevine kaldırma kuvveti etki eder demek akademik olarak doğru olmaz. bay_fzk ?
Hem genel bilgi hem de “coriolis” anahtar kelimesi için teşekkür ediyorum. Mutlaka okumalar yapacağım.
Aslında fizikle alakalı bir uğraşım yok, biraz uzak bir alanda çalışıyorum. Yeğenlerime ders vermek için önce kendim çalışıyorum. Biraz detaycı olunca daha doğrusu işin felsefesi ve matematiğine kafayı takınca takılıp kalıyorum 🙂
O yüzden bu konuları çalışırken çok faydalı bilgilere de ulaştım sayenizde. Neredeyse diğer bütün benzer sitelerde soru çözüp bırakıyorlar ki ne yazık ki soru çözmeyi öğretse de daha öteye geçemiyor. Umarım bu anlatım tarzınız ilk okul seviyesinde de çocuklara ulaşıyordur. Böylece en sevilmeyen derslerden biri olmaktan çıkıp, farklı bir konuma gelir Fizik dersi ve dünyası tüm yetişen öğrenciler için. Hatta benzer yaklaşımlarla diğer derslerin de içerikleri geliştirilirse inanılmaz mutluluk duyarım. Başarılarınızın devamını diliyorum, en kısa zamanda içeriklerin tamamlanmasını da bekliyorum. Ben de çevremdeki herkese buraya önererek ufak da olsa bir katkı da bulunmaya çalışıyorum.
Merhaba size bir sorum olacak ;
http://hizliresim.com/LDO9Jz
Bir yayın ucuna bağlı olan taş dairesel biçimde çevriliyor
Yayın boyu hangi açıda ne olur?
Merkezcil kuvveti sağlayan yayın gerilmesi. Yayı düşey doğrultuda çeviriyorsak, tepe noktasında yayın gerilme kuvveti azalır, en alt noktada artar.
Teşekkür ederim güzel yazı olmuş. Serbest cisim diyagramı baya işime yaradı.
Bu konu çok daha güzel olmuş. Tebrikler
Basit harmonik hareket ve diğer konuları ne zaman yayınlayacaksınız
Yakın bir zamanda.
Basit harmonik hareket hala neden yayınlanmadı?
Yakında yayınlanacak diye düşünüyorum.
Bişey söylemek istiyorum fiziki burdan öğrendim lütfen devam eden size umut bağlamış biri olarak söylüyorum lütfen ayt konularını yükleyin sınava girecez az kaldı lütfen
Belki hocanın başka işi de olduğundandır?
Hocam düşeyde düzgün çembersel hareket yapan cisimde net tork sıfırmıdır
Düzgün çembersel hareketse, açısal ivme sıfırdır, bu nedenle tork da sıfırdır.
Sorduğun bu soru 27 haziran 2021 ayt sorusuydu, müneccim gibisin.
Hocam düşey olarak çembersel hareket yapan cisimde tork oluşacağı için açısal momentum korunmaz değil mi? Birde bu cisme düzgün çembersel hareket yaptırmak için havanın sürtünme kuvvetini kullanabilirmiyiz?
Evet, eğer açısal hız sabit kalmazsa tork oluşur, açısal momentum değişir. Havanın sürtünme kuvveti bazen artıran bazen azaltan yönde uygulanacağı için biraz zor geliyor bana.
bir şey söylemek istiyorum, lütfen arada sorduğunuz veya meydan okumalardaki soruların cevaplarını yazar mısınız? cidden merak ediyorum içimde kalıyor , teşekkürler
Cevapları okuyuculardan bekliyoruz. Cevaptan çok üzerinde düşünmek önemli.
Hocam merhaba, çembersel harekette merkeze doğru bir kuvvet oluyor ya işte bu kuvvet cismi neden merkeze doğru çekmiyor? Cismin hızından dolayı yörüngeden dışarı çıkmaya çalışması ile mi bu kuvvet dengeleniyor? Ama bu sefer de ivme olmazdı tam içinden çıkamadım yardım eder misiniz?
Çembersel hareketteki merkeze doğru olan kuvvet cismi merkeze doğru çekiyor. Bu bir ivmeye neden oluyor, ama ivme cismin süratinde değil hızının yönündeki değişim oluyor. Merkeze doğru olan kuvvet dengelenmiyor, dengelenseydi cisim doğrusal olarak hareket ederdi, yönü değişmezdi. Hızın yönünün değişmesine merkezcil ivme diyoruz.
hocam fsürtünme neden içeri doğru oluyo ben anlamadım biraz açıklayabilir misiniz?
Eğer net kuvvet içeri doğru olmasa mum dümdüz giderdi, ama gitmiyor. Demek ki bir kuvvet mumu içeri doğru itiyor. Bu kuvvet masayla temas eden mumun tabanına uygulanan sürtünme kuvveti.
Kovadaki suyun dökülmeme sebebi fm nedeniyle ilgili mi sonuç olarak merkezden dışarı doğru bir kuvvet var aşağıya doğru ise m ve g var bu ikisini dengeleyen ise fm diye düşündüm
Cevap verirseniz merakımı giderirseniz çok mutlu olurum hocam
Dışarıdan bakarsak (eylemsiz gözlem çerçevesinden) kovadaki suyun içinde dışarı doğru kuvvet yok, aksine kovanın ağırlığı artı kova suyu aşağıya itiyor. Kovanın dönebilmesinin nedeni bu merkeze doğru olan kuvvet.
Eylemli gözlem çerçevesinden bakarsak suya merkezkaç kuvveti etki eder. Sanırım bundan dolayı düşmüyor.