Kaldıraç nedir çeşitleri nelerdir?

Archimedes’in (Arşimet) ünlü sözü “Bana bir destek noktası verin, Dünya’yı yerinden oynatayım.” kaldıraç sistemini anlatır. Kaldıraç, bir çubuk ve bu çubuğun bir destek noktası etrafında dönebilmesi ilkesine göre tasarlanmış bir basit makinedir. Kaldıraçlarda üç unsur bulunur: destek noktası, yük ve kuvvet. Kaldıraçlar bu üç unsurun birbirine göre konumuna göre üç çeşittir. Şimdi kaldıraç türlerini inceleyelim.

Desteğin Yük ile Kuvvet Arasında Olduğu Kaldıraçlar

Aşağıdaki şekilde 1. tip ya da destek noktasının yük ile kuvvet arasına yerleştirildiği kaldıraç türü gösteriliyor. Çubuğun ağırlığını ihmal ediyoruz. Çubuğun bir ucuna yükü yerleştiriyoruz öbür ucundan kuvvet uyguluyoruz. Günlük hayatta tahtıravalli, makas, pense ve eşit kollu terazi bu tür kaldıracın örnekleri arasında.

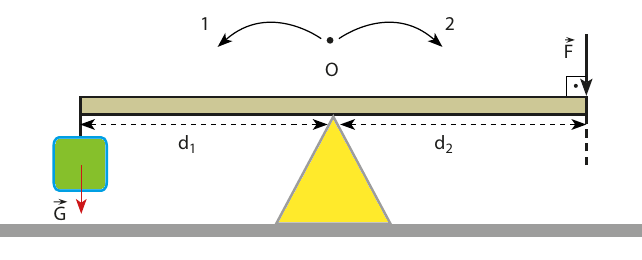
Şimdi bu kaldıracı biraz daha yakından inceleyelim. Çubuk O noktası etrafında dönebiliyor. Eğer bu sistem dengede ise O noktasına göre net torkun sıfır olması lazım.
\vec{\tau}_{toplam} = \vec{\tau}_G + \vec{\tau}_F

G ağırlığının çubuğu 1 yönünde, F kuvvetinin ise 2 yönünde döndürdüğüne dikkat edin. Öyleyse:
G \times d_1 = F \times d_2

d₁ < d₂ ise F < G olur, yani yükü kaldırmak için yükün ağırlığından daha küçük bir kuvvet yeterli olur. Ama kuvvetten kazanç olduğu için yoldan kaybediyoruz. d₁ = d₂ ise F = G olur, bu durumda kuvvetten kazanç olmaz.

Eğer çubuğun ağırlığını ihmal etmezsek, tork denklemine çubuğun ağırlığını da eklemek gerekir. Desteğin bulunduğu yere göre G ile F ilişkisi değişebilir.

Yükün Destek ile Kuvvet Arasında Olduğu Kaldıraçlar

Aşağıdaki şekilde 2. tip ya da yükün destek noktasıyla kuvvet arasında olduğu kaldıraç türü görülüyor. Yine çubuğun ağırlığının olmadığını kabul edilyoruz. Bu kez çubuğun bir ucuna desteği koyuyoruz, ortaya yükü yerleştiriyoruz, çubuğun diğer ucundan kuvvet uyguluyoruz. Günlük yaşamda el arabası, şişe kapağı açacağı ve ceviz kıracağı gibi araçlar bu tür kaldıracın örnekleri.

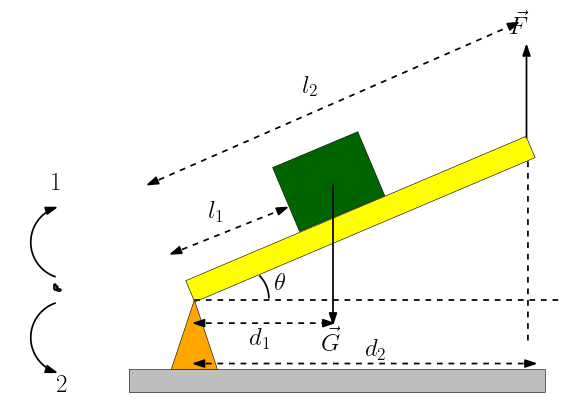
Şimdi bu kaldıraca daha yakından bakalım. Tıpkı bir önceki kaldıraçta yaptığımız gibi denge durumunda torkun sıfır olduğu ilkesini kullanacağız.
\vec{\tau}_{toplam} = \vec{\tau}_G + \vec{\tau}_F

Bu kez G ağırlığının çubuğu 2 yönünde, F kuvvetinin ise 1 yönünde döndürdüğüne dikkat edin. Öyleyse:
G \times d_1 = F \times d_2

Ayrıca d₁ ve d₂ dönme noktasına dik uzaklıklar. Bu uzaklıkları çubuğun boyu cinsinden de yazabiliriz.
d_1 = l_1 cos \theta; \space d_2 = l_2 cos\theta

Bir önceki denklemde yerine koyarsak:
G l_1cos\theta = Fl_2cos\theta

G \times l_1 = F \times l_2

Çubuğun uzunluğuyla destek noktasına uzaklık arasındaki ilişkinin birinci tip kaldıraçta da aynı olduğunu fark ettiniz mi?

Bu tür kaldıraçlarda her zaman d₁ < d₂‘dir. Bu nedenle daima F < G olur. Yükü kaldırmak için gereken kuvvet hep yükten az olur. Ama kuvvetten kazanç olduğu oranda yoldan kayıp vardır.

Kuvvetin Destek ile Yük Arasında Olduğu Kaldıraçlar

Aşağıdaki şekilde 3. tip ya da kuvvetin dayanak (destek) noktasıyla yük arasında olduğu kaldıraç türü (bir küpşeker maşası) görülüyor. Tekrar çubuğun ağırlığının olmadığını farz edilyoruz. Çubuğun bir ucuna desteği koyuyoruz, çubuğun diğer ucuna yükü koyuyoruz, ortadan da kuvvet uyguluyoruz. Günlük yaşamda tırnak makası, maşa, cımbız ve kürek bu tür kaldıracın örnekleri.

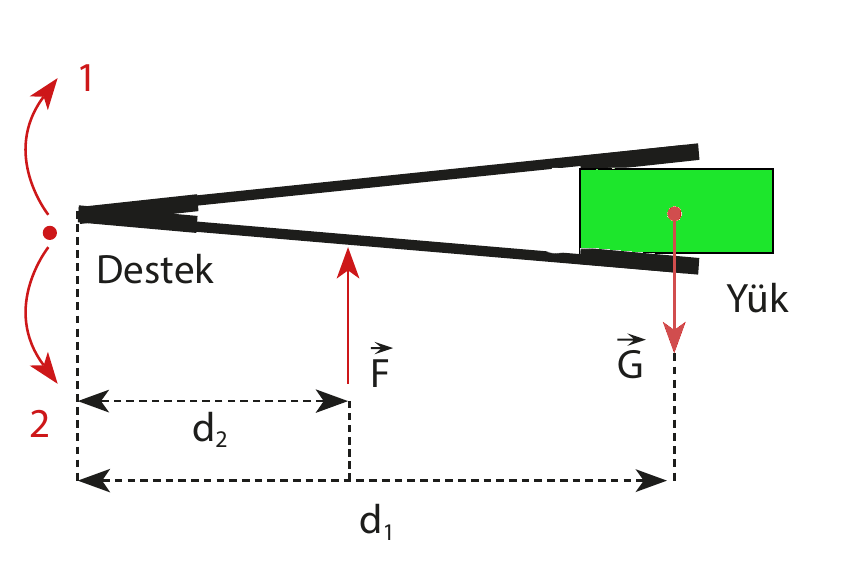
Şimdi de bu tür kaldıracı yakından inceleyelim. Yine denge durumunda torkun sıfır olduğu prensibinden yola çıkacağız.
\vec{\tau}_{toplam} = \vec{\tau}_G + \vec{\tau}_F

G ağırlığının çubuğu destek noktası etrafında 2 yönünde, F kuvvetinin ise 1 yönünde döndürdüğüne dikkat edin. Öyleyse:
G \times d_1 = F \times d_2

Bu durumda her zaman d₂ < d₁ olduğundan G < F olur. Yani yükü kaldırmak için yükten daha büyük bir kuvvet uygulanır. Kuvvetten kayıp oranında yoldan kazanç vardır.

Örnek soru

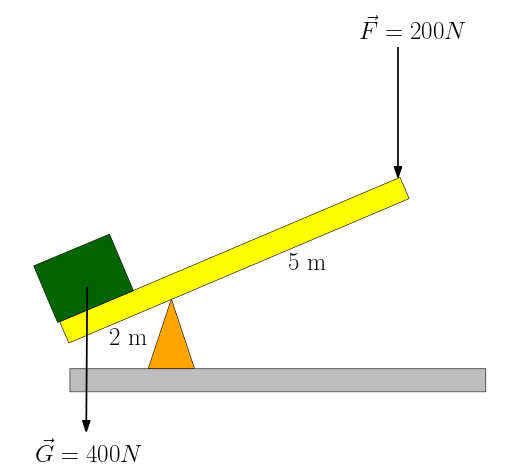
Ağırlığı ihmal edilen bir çubuk üzerinde olan 400 N ağırlığındaki türdeş bir cisim, 200 N büyüklüğündeki kuvvetle şekildeki
gibi dengeleniyor. Bu kaldıracın verimi nedir?

Çözüm

Kuvveti uyguladığımızda sistem dengede, soru bize bunu söylüyor. Dengedeyse Newton’un eylemsizlik yasasına göre yük sabit hızla yukarı hareket ediyor demektir. Hareketi esnasında yük yerden h₁ kadar yükselmiş olsun. Kaldıracın öbür ucu ne kadar alçalmış olur?
h_1 = l_1 cos \theta; h_2 = l_2 cos \theta

Şimdi yapılan işleri bulalım:
W_G = 400 \times h_1; W_F = 200 \times h_2

Şimdi verimi yazalım:
Verim = \frac{400 \times 2 cos \theta}{200 \times 5cos\theta} = \frac{4}{5} = \%80

Kaldıraçlarla ilgili kazanımlar

11.1.10.1. Günlük hayatta kullanılan basit makinelerin işlevlerini açıklar.

• Kaldıraç, sabit ve hareketli makara, palanga, eğik düzlem, vida, çıkrık, çark ve kasnak ile sınırlı kalınır.

11.1.10.2. Basit makineler ile ilgili hesaplamalar yapar.

• İkiden fazla basit makinenin bir arada olduğu sistemlerle ilgili matematiksel hesaplamalara girilmez.
• Hesaplamaların günlük hayatta kullanılan basit makine örnekleri (anahtar gibi) üzerinden yapılması sağlanır.
• Basit makinelerde verim ile ilgili matematiksel hesaplamalar yapılması sağlanır.