Kütle çekim kuvvetini ve alanını öğrendikten sonra sıra kütle çekim potansiyel enerjisine geldi. Potansiyel enerjinin bir cismin sadece konumundan dolayı sahip olduğu enerji türü olduğunu hatırlayın. Tam olarak şöyle anlatabiliriz. Elimizde iki kütle olsun. Bu kütlelerden birini sonsuz uzaklıktan diğerine R kadar yaklaştırmak için yapılması gereken işe potansiyel enerji diyoruz. Aşağıdaki resimde bu iki kütleyi görüyoruz.
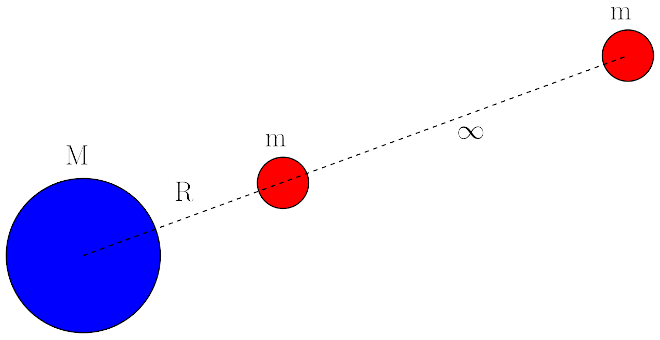
Kırmızı m kütleli cisim sonsuzdayken üzerine etkiyen kütle çekim kuvveti sıfır, çünkü mesafe arttıkça kuvvet azalıyor. Dolayısıyla kırmızı cismin sonsuzdaki enerjisi sıfır. Ama kırmızı cisim mavi cisimden R kadar uzakta olduğu zamanki enerjisi sıfır değil. Enerjisini kırmızı cismi bulunduğu yere çıkarmak için yapılan işten bulabiliriz:
E = W = FxNeden F aldık? Çünkü, cismi x’e getirmek için bizim uyguladığımız kuvvet kütleçekim kuvvetinin zıt yönünde olmak zorunda, yani soldan sağa doğru. Yer değiştirme de soldan sağa doğru.
E = Fx = G\frac{mM}{R^2}R = G\frac{mM}{R}Şimdi de potansiyel enerjisini tanımlayabiliriz yani formülünü bulabiliriz:
W_{\infty} = Fx; R = \infty; F_{\infty} = 0; E_{\infty} = 0
Eksi işaretli (negatif) potansiyel enerji nasıl olabilir? Basit bir açıklaması var. İki cismin birbirlerine göre bir konumdaki potansiyel enerjisi, cisimlerin sonsuzdaki potansiyel enerjisinden daha küçük demek sadece.
Bu durumda bir cisim Dünya’da yerden belli bir yükselikte olduğunda da bir potansiyel enerjisi olmalı, çünkü üstüne kütle çekim kuvveti uygulanıyor. Aşağıdaki resimde m kütleli bir cisim yeryüzünden h yüksekliğinde duruyor. Dünyanın kütlesini M yarıçapını R olarak alıyoruz. Şimdi kütle çekim potansiyel enerjisini ve formülünü inceleyelim.
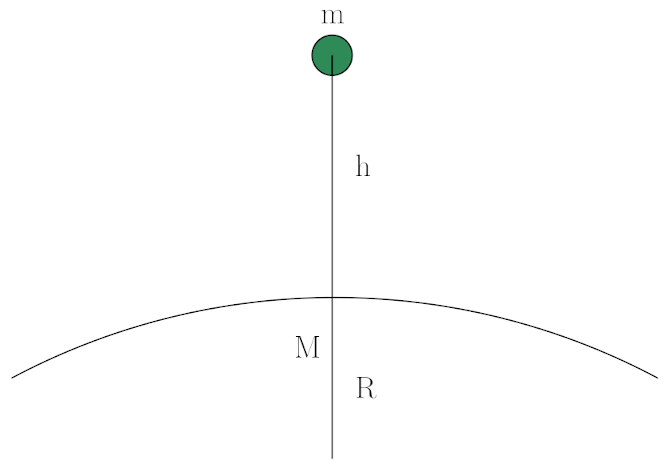
Potansiyel enerji bu cismi sonsuz uzaklıktan bulunduğu yerden h yüksekliğine getirmek için yapılan işe eşit. Cismi bulunduğu yüksekliğe (yüksekliği yeryüzünden alıyoruz, Dünya’nın merkezinden değil) getirmek için yapılan iş:
W = Fx = G\frac{mM}{(R+h)^2}h
Son olarak yapılan işin sonsuzdan olduğu noktaya getirilmek için olduğunu yazalım:
E_P = E_{\infty} - E_P = 0 - G\frac{mM}{(R+h)^2}h = - G\frac{mM}{(R+h)^2}h
Potansiyel enerjinin eksi olduğunu bulduk. Çünkü kütle çekim cisimleri çeken bir kuvvet, eğer iki aynı yük gibi iten bir kuvvet olsaydı o potansiyel enerji zaman artı olurdu. Tam tersini düşünün bir de. Cisimleri birbirinden ayırmak için, yani bir cismi sonsuza götürmek için pozitif iş yapmanız gerekir. Az sonra kurtulma enerjisinde göreceğiz.
Yüksekliğin Dünyanın yarıçapından çok küçük olduğunu ( h << R, R + h = R diyeceğiz) ve kütle çekim alanını hatırlarsak:
E_P = -m (G\frac{M}{R^2})h; g = G\frac{M}{R^2}; E_P = -mgh
Daha önce yerçekimi potansiyel enerjisini mgh olarak öğrenmiştiniz, şimdi bu formülün nereden geldiğini öğrenmiş oldunuz.
Eğer h yeterince büyükse, örneğin bir kaç yüz kilometre civarındaysa kütle çekim alanını önemli derecede etkiler, bu nedenle formülün orjinalini yani R+h’yi kullanmamız gerekir.
Bağlanma enerjisi nedir?
İki kütleden oluşan bir sistemde kütlelerden birinin bulunduğu konumdaki toplam enerjisine bağlanma enerjisi denir. Örneğin, Dünya’nın etrafında yörüngede dolanan bir uydunun yörüngesinin değişmeden harket edebilmesi için gerekli olan enerji o uydunun bağlanma enerjisidir. Şimdi bu enerjiyi tam olarak bulabiliriz. Uydunun çembersel yörüngede kalmasını sağlayan merkezcil kuvvet kütle çekim kuvveti. Newton’un ikinci hareket yasasından kuvvet kütle ile merkezcil ivmenin çarpımına eşit:
F = ma
Buradan hızın karesini bulalım:
v^2 = G\frac{M}{R}
Uydunun kinetik enerjisi:
E_K = \frac{1}{2}mv^2 = \frac{1}{2}G\frac{Mm}{R}
Cismin toplam enerjisi kinetik ve potansiyel enerjilerinin toplamına eşit.
E_T = E_K + E_P
Potansiyel enerjinin eksi olduğuna dikkat ederek yazalım.
E_T = \frac{1}{2}G\frac{Mm}{R} + (-G\frac{mM}{R^2})
Bu durumdaki toplam enerjiye bağlanma enerjisi demiştik. Öyleyse bulduğumuz şey de bağlanma enerjisi:
E_B = - \frac{1}{2}G\frac{Mm}{R}
Bağlanma enerjisinin eksi işaretli olduğuna ve büyüklüğünün potansiyel enerjinin yarısına eşit olduğuna dikkat edin.
Kurtulma enerjisi nedir?
İki kütleden oluşan bir sistemde kütlelerden birinin diğerinin çekim kuvvetinin etkisinden tamamen kurtulması için verilmesi gereken en küçük enerjiye de kurtulma enerjisi denir. Uydunun Dünya’nın yerçekiminden tamamen kurtulması için gereken en az enerji de kurtulma enerjisidir. Uydunun Dünya’nın çekim alanından kurtulması demek aldığı enerjiyle sonsuz uzaklığa girmesi yani çekim kuvvetinin sıfır olacağı yere varması demektir. Bu tanımın potansiyel enerji tanımının neredeyse aynısı olduğuna sadece işaretin değiştiğine dikkat edin.
Enerjinin korunumundan ilk enerjinin son enerjiye eşit olduğunu biliyoruz. Ayrıca cismin sonsuzdaki kinetik ve potansiyel enerjisinin (çünkü sonsuz uzaklıkta) de sıfır olacağını biliyoruz.
E_{ilk} = E_{son}
Öyleyse:
\frac{1}{2}mv^2 = G\frac{mM}{R}
O zaman cismin kurtulma hızını da bulabiliriz:
v^2 = 2G\frac{M}{R}
Kurtulma hızının cismin kütlesinden bağımsız olduğuna dikkat edin.
Kurtulma enerjisi Newton’un bir düşünce deneyinin ürünü. Yüksek bir dağın tepesinden bir top mermisini çeşitli hızlarla fırlattığımızı düşünelim. Eğer yeterince hızlı atmazsak top mermisi yatay atış hareketi yapar, düşeyde sabit ivmeli hareket yaparak yere düşer. Ama yeterince hızlı atarsak mermi sürekli düşmeye devam eder ve çembersel hareket yapmaya başlar. Yörüngede dolanan uydular aslında sürekli Dünya’ya düşüyorlar, ama o kadar hızlılar ki yere varamıyorlar.
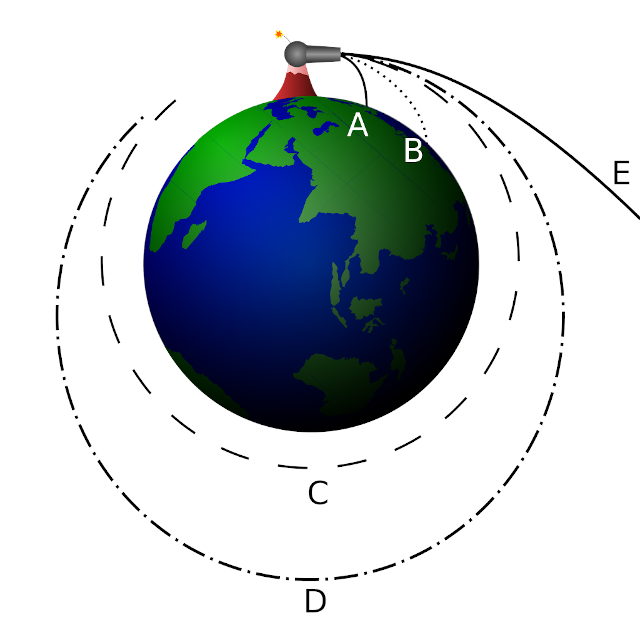
Dünya’dan kurtulma hızını hesaplayarak bitirelim. Bir roket için yüzeyden kurtulma hızı:
v = \sqrt{\frac{2GM}{R}}
Dünyanın kütlesini ve yarıçapını ve evrensel çekim sabitini yerine koyalım:
v = \sqrt{\frac{2 \times 6,67 \times 10^{-11} \times 5,972 \times 10^{24}}{6,371 \times 10^6}} = 11,18 \times 10^3 m/s = 11,2 km/s
Yani Dünya’dan kurtulması için roketin ses hızından 33 kat ve bir mermiden 10 kat aha hızlı gitmesi gerekiyor.
Kütle çekim potansiyel enerjisiyle ilgili kazanımlar
12.1.4.3. Kütle çekim potansiyel enerjisini açıklar.
- Bağlanma ve kurtulma enerjisi kavramları üzerinde durulur.