Düzgün çembersel harekette, hareket eden cismin çizgisel süratinin sabit olduğunu ama çizgisel hızının sürekli değiştiğini, çünkü yönünün değiştiğini biliyoruz. (Sürat ve hız arasındaki farkı hatırlamak isteyebilirsiniz.) Hız vektörünün zamana göre değişimine ivme dendiğini de biliyoruz. Düzgün çembersel harekette ivme vektörünün yönünün her zaman, hareketin yörüngesi olan çemberin merkezine doğru olduğu ve cismin çizgisel hızına daima dik olduğu çıkarımını da yaptık, buna merkezcil ivme dedik. Şimdi, merkezcil ivmeye neden olan kuvveti, merkezcil kuvvet nedir sorusunu inceleyeceğiz. Newton’un Hareket Yasalarının ikincisi bize eğer ivme varsa net kuvvet var diyor. Net kuvvetin yönünün de her zaman ivme vektörüyle aynı yönde olduğunu söylüyor. Bu arada başlıkta var, ama aslında gerçek bir kuvvet olmayan bir de merkezkaç kuvveti kavramı var, bunu da inceleyeceğiz.
Merkezcil kuvvet nedir? Nelere bağlıdır? Formülü nasıldır?
Merkezcil kuvveti anlamak için kuvvet ve hareket arasındaki ilişkiyi tekrar incelememiz gerekiyor. Hareketin gizemini çözen Newton’un hareket kanunlarını hatırlayalım:
- Bir cismin hareket etmesi için üzerinde net kuvvet olması gerekmez. Net kuvvet sıfırken de bir cisim sabit hızla (yönü ve şiddeti değişmeden) yani ivmesiz olarak hareket edebilir. Öyleyse bir cismin doğal hareketi, yani üzerindeki net kuvvet sıfırken hareketi, düz bir çizgi boyunca sabit hızla ilerlemektir.
- Bir cismin üzerinde net kuvvet varsa (sıfırdan farklıysa) mutlaka ama mutlaka ivmelenir, yani hızı zamana göre değişir. Hız değişimi şiddetinin değişimi (hızlanması ya da yavaşlaması) olabileceği gibi, yönünün değişmesi de olabilir. Eğer bir cisim ivmeli hareket yapıyorsa, ivmeye sebep olan bir kuvvet olmak zorundadır. Yoksa ivmelenemez. \vec{F} = m\vec{a} bu demektir.
Düzgün dairesel hareket yapan bir cismin ivmelendiğini biliyoruz, çünkü hızının şiddeti (sürati) değişmese de yönü sürekli değişiyor. İvmenin yönü merkeze doğru olduğuna göre, ivmeyle aynı yönde bir net kuvvet olmak zorunda. Olmasa cisim çembersel bir yörünge izleyemez, bir doğru üzerinde ilerler. Eğer bir şey düzgün çembersel hareket yapıyorsa, cismi merkeze doğru iten ya da çeken bir kuvvet olmak zorundadır, yoksa çembersel hareket yapamaz.
Aşağıdaki resimde bir hulahopun (kasnak) içinde çembersel hareket yapan bir top görünüyor. Topun çembersel yörüngede hareketine devam edebimesinin nedeni hulahopun duvarının topu sürekli içeriye doğru itmesi. Hulahopu kaldırdığımız zaman top dönmeyi bırakıyor, çünkü topun yönünü değiştirecek, merkeze itecek bir kuvvet kalmıyor. En son hızının yönünde düz bir çizgi üzerinde hareket etmeye başlıyor, düzgün doğrusal hareket yapıyor ve kutuya çarpıyor.

Aşağıdaki resimde de bir kız bir ipin ucuna bağladığı anahtarı başının üstünde çeviriyor. Anahtarın düzgün çembersel hareket yapabilmesinin nedeni ipin anahtarı sürekli merkeze doğru çekiyor olması. Kız ipi bırakırsa veya ip koparsa, anahtar hızının en son yönünde düz bir doğru üstünde hareket ediyor.
Merkezcil ivmenin sebebi olan merkezcil kuvveti bulmamız için Newton’un ikinci hareket yasasını yazmamız yeterli. Merkezcil kuvvetin formülü:
\vec{F}_{merkezcil} = m \vec{a}_{merkezcil} \vec{a}_{merkezcil} = \frac{v^2}{r} \vec{F}_{merkezcil} = m \frac{v^2}{r}m cismin kütlesini, v çizgisel süratini (çizgisel hızının büyüklüğünü), r çemberin yarıçapını gösteriyor.
Yani merkezcil kuvvet cismin kütlesiyle doğru orantılı, çizgisel süratinin karesiyle doğru orantılı ve dönme yarıçapıyla ters orantılıdır.
Merkezcil kuvveti bir de açısal hız cinsinden yazalım:
v=\omega r \vec{F}_{merkezcil} = m \frac{v^2}{r} \vec{F}_{merkezcil} = m\frac{w^2r^2}{r} = mr\omega^2Biraz daha oynayabiliriz, frekans ve periyot cinsinden merkezcil kuvveti yazabiliriz:
\omega = 2\pi f = \frac{2 \pi} {T} \vec{F}_{merkezcil} = mr 4 \pi^2f^2 = \frac{mr 4 \pi^2}{T^2}Son olarak merkezcil kuvvet ifadesindeki merkezcil kelimesi sadece kuvvetin yönü anlamına geliyor, yani kuvvetin yönü çemberin merkezine doğru demek. Ama kuvvetin kaynağı, ip gerilmesi, duvarın itmesi, normal kuvveti, sürtünme, kütle çekimi ya da elektriksel kuvvet olabilir. Size verilen problem durumlarını dikkatlice inceleyerek kuvvetin kaynağı ile yönü arasındaki ilişkiyi kurmanız gerekir.
Merkezkaç kuvveti nedir?
Merkezkaç kuvveti gerçek bir kuvvet değildir. Eylemli gözlem çerçevelerinde hissedilen, ama eylemsiz gözlem çerçevelerinde gözlenmeyen hayalet bir kuvvet olarak tanımlanır. Arabanın içinde virajı dönerken dışa doğru savrulduğunuzu hissedersiniz. Sanki bir kuvvet sizi virajın merkezinden dışarı doğru itiyor gibidir. Ama aslında arabanın dışarısından bakan birine göre öyle bir kuvvet yoktur. Siz eylemsizlikten dolayı düz bir yol boyunca hareket etmeye meylederken, arabanın koltuğu ya da kapısı, size çemberin merkezine doğru bir kuvvet uygulayarak yönünüzü değiştirir.
Sizin arabanın içinde hissettiğiniz şey, aslında hızlanan bir arabada üzerinizde geriye doğru bir kuvvet, yavaşlayan bir arabada ileri doğru bir kuvvet varmış gibi hissetmenizle aynı şeydir. Bu hayalet kuvvete bazı kitaplar eylemsizlik kuvveti diyor, ama öyle bir kuvvet gerçekte yok. Çünkü ne hızlanan, ne yavaşlayan, ne de virajı dönen bir arabanın içinde net kuvvet sıfır, çünkü hepsi ivmeleniyor. Net kuvvet sıfır değilse ivme var demektir. Eğer eylemsizlik kuvveti ya da merkezkaç kuvveti var olsa, merkezcil kuvveti dengelemesi ve net kuvvetin sıfır olması gerekir. O zaman ivme olmaz. Ama üç durumda da ivme var.
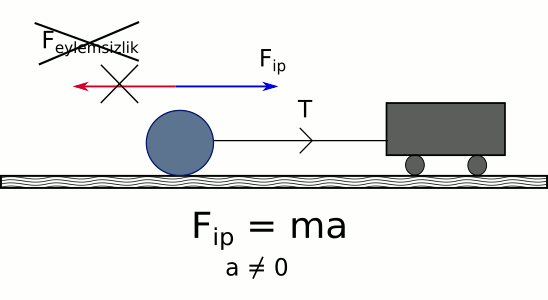
Aşağıdaki resimde bir araba bir topu çekiyor, çektiği için ivmelendiriyor. Topun üstündeki net kuvvet ip gerilmesinden kaynaklanan T = Fip. Eğer eylemsizlik kuvveti olsaydı, Fip‘i dengelerdi, net kuvvet sıfır olurdu, ivme olmazdı. Ama ivme var. Fip = mtopa.
Aşağıdaki resimde de bir iple yatay düzlemde çevirilen, düzgün çembersel hareket yapan bir top görülüyor. Bu topun dönmesinin nedeni iple içeri doğru çekiyor olmamız. Eğer çekmeyi bırakırsak top fırlar gider, düz bir doğru boyunca hareket eder. Çektiğimiz için topun hızını (yönünü) sürekli değiştiriyoruz, yani top ivmeleniyor. Eğer merkezkaç kuvveti olsaydı, ipin kuvvetini dengelerdi ve ivme sıfır olurdu, top dönmezdi. Ama dönüyor. Yani merkezkaç kuvveti diye bir şey yok. Sadece merkezcil kuvvet var.
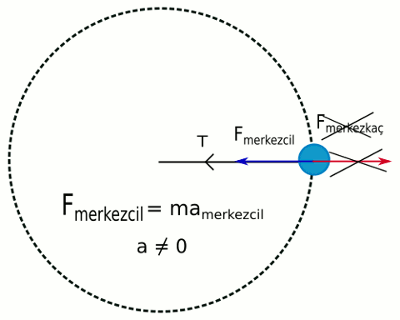
Çembersel hareket yapan bir cisme etkiyen hareket doğrultusuna dik net kuvvet ortadan kalktığında cisim çembersel hareket yapmaya devam edemez. Çembersel yörüngede hareket eden cisimlere merkezkaç kuvveti etki etmez.
Merkezcil Kuvvet ile ilgili örnek sorular, problemler ve çözümleri
Soru 1: Merkezcil kuvveti hesaplama
Kütlesi 2 kg olan bir cisim yarıçapı 60 cm olan bir çembersel yörüngede düzgün çembersel hareket yapmaktadır. Cisim 4 saniyede 10 turu tamamladığına göre cisme etkiyen merkezcil kuvvet kaç Newtondur? (π = 3 alın.)
Çözüm:
Aradığımız şey merkezcil kuvvet, tanımını yazarak başlayalım:
Kütleyi ve yarıçapı biliyoruz, çizgisel hızı bulmamız lazım. Onun için de açısal hızı bulmalıyız:
v=\omega r; \space \omega = 2\pi fFrekansın tanımını hatırlayalım: Bir saniyede kaç tur atıldığı yanı tur sayısı/geçen süre:
f = \frac{10}{4\space s}=2,5 \space s^{-1} \omega = 2 \pi(2.5 \space s^{-1}) = 15 \space rad/s^{-1}Artık çizgisel hızı bulmak kolay yerine koyalım:
v = 15 \space \times 0,6 m/s = 9 \space m/sŞimdi de merkezcil kuvveti hesaplayalım:
F_{merkezcil} = 2\frac{9^2}{0,6} = 270 \space NSoru 2: Merkezcil kuvvet oranı
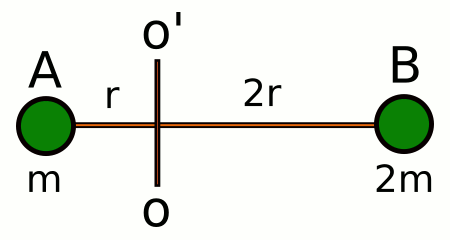
Boyutları küçük, kütleleri sırasıyla m ve 2m olan A ve B cisimleri, kütlesi önemsiz ve esnek olmayan bir çubuğun uçlarına şekildeki gibi yapıştırılmıştır. Düzenek düşey O – O’ ekseni etrafında yatay düzlemde serbestçe dönmektedir. A cisminin dönme eksenine uzaklığı r, B cismininki 2r‘dir.
A cismine uygulanan merkezcil kuvvet F ise, B cismine uygulanan merkezcil kuvvet kaç F’dir?
Çözüm:
Önce A cismine uygulanan merkezcil kuvveti hesaplayalım:
F = m\frac{v_A^2}{r}Sonra bulmak istediğimiz B cismine uygulanan merkezcil kuvveti yazalım:
F_B = 2m\frac{v_B^2}{2r} = m\frac{v_B^2}{r}Bizden bu ikisinin oranı isteniyor:
\frac{F_B}{F}=\frac{\frac{mv_B^2}{r}}{\frac{mv_A^2}{r}}Sadeleştirirsek:
\frac{F_B}{F}=\frac{v_B^2}{v_A^2}Bulmamız gereken oran B cisminin çizgisel süratinin karesinin, A cisminin çizgisel süratinin karesine oranı.
Şimdi bu iki cismin birlikte döndüğünü fark etmeliyiz. İkisi de aynı periyotla dönüyorlar, bir turu aynı sürede tamamlıyorlar. Dolayısıyla açısal hızları da aynı olmak zorunda:
T_A = T_B \space ; \space w = \frac{2\pi}{T} öyleyse:
\omega_A = \omega_B = \omegaÇizgisel sürati açısal hız cinsinden yazabiliriz:
v = \omega r v_A = \omega r \space; \space v_B = \omega (2r)Şimdi oranı yazalım:
\frac{F_B}{F}=\frac{v_B^2}{v_A^2}= \frac{4\omega^2r^2}{\omega^2r^2}=4Öyleyse:
F_B = 4FMerkezcil Kuvvet ile ilgili Simülasyon
Düzgün Çembersel Hareket Simülasyonu – Sanal deney ile merkezcil kuvvetin bağlı olduğu değişkenleri araştırabileceğiniz klasik bir laboratuvar uygulaması var, bir bakmalısınız.
Merkezcil Kuvvet ile ilgili Kavram Yanılgıları
- Sabit süratle çembersel hareket yapan bir cismin ivmesi sıfırdır. (ivme sıfır değildir, hızın yönü değişiyor, dikkatli olun.)
- Çembersel hareket yapan bir cisme etkiyen hareket doğrultusuna dik net kuvvet ortadan kalktığında cisim çembersel hareket yapmaya devam eder. (Çembersel hareket için merkezcil kuvvet şarttır, olmazsa cisim dönemez, düz bir doğru boyunca ilerler.)
- Çembersel yörüngede hareket eden cisimlere merkezkaç kuvveti etki eder. (Merkezkaç kuvveti diye bir şey yok.)
Merkezcil Kuvvet ile ilgili Kazanımlar
2017 – 12.1.1.2. Düzgün çembersel harekette merkezcil kuvvetin bağlı olduğu değişkenleri analiz eder.
- Deney yaparak veya simülasyonlarla merkezcil kuvvetin bağlı olduğu değişkenler arasındaki ilişkinin belirlenmesi sağlanır. Matematiksel model verilir. Matematiksel hesaplamalar yapılır.
Merkezcil Kuvvet ile ilgili MEB ve EBA Testleri
- Düzgün Çembersel Hareket Test 2 (2016 – 2017)
Son soru:
Merkezcil kuvvet düzgün çembersel hareket yapan bir cismin kinetik enerjisini değiştirebilir mi? Yorumlara cevabınızı yazabilirsiniz.
Şuana kadar gördüğüm en iyi fizik öğreten site. Tebriklerimi ve teşekkürlerimi sunuyorum yapımında emeği geçenlere.????
Memnun olduğunuza sevindim. Daha yazılacak çok konu var.
FİZİK öğretmeni olarak sitenizi çok beğendim. Çok güzel anlatmışsınız. Teşekkürler.
Teşekkür ederim. Daha yazacaklarım var.
son soruyu cok merak ettim. lütfen acıklarmısınız
Merkezcil kuvvet her zaman çizgisel hızın yönüne diktir, dolayısıyla yer değiştirmeye (∆x) de diktir. İşin tanımı W=F∆xcosθ olduğu için ve daima θ=90° (cos90° = 0) olacağı için yapılan iş hep sıfır olur. ∆K.E. = W = 0, kinetik enerjiyi merkezcil kuvvet değiştiremez, düzgün dairesel harekette iş yapılmaz.
Merak ettiğim bir şey var. Dairesel hareket yaptırılan yatay bir sistem düşünürsek örneğin ucunda ağırlık olan bir ipi elimizle yatay konumda döndürüyoruz sisteme merkezcil kuvvet ve yerçekimi kuvveti etki edecek ama sistem yatayda dengede durmaya devam edecek bu durumda yerçekimine karşı yönde bir kuvvet olsun ki sistemi böyle dengede tutsun diye düşünüyorum. Ya da bir bardağın içine bir cisim bırakıp bardağı hızlıca döndürdüğümüzü düşünürsek cisim git gide yükselecektir. Özetle oluşan bu kuvvet nedir?
Çok zekice bir soru, benim de aklıma gelmişti. Elinde bir ipi çevirirsen aslında ucundaki taş hiç bir zaman yere tam olarak yatay olmaz. Hep biraz açı yapar, çünkü ağırlığı dengeleyecek bir kuvvet yok. Konik sarkaç diyoruz buna. Bardaktaki pinpon topuna gelince. Silindir bir bardaktan söz ediyoruz. Eğer bardağı sadece yatayda çevirmeye devam edersen, yani topa uygulanan kuvvetin hiç dik bileşeni olmazsa top yükselmez. Bunu evde bir dene, ama dikkat et bardağı eğmemen lazım hiç. Bir de topun bardağın içindeyken serbest cisim diyagramını çiz. Sonuçlarını bekliyorum.
Bir proje için çizim üzerinde size merkezcil kuvvet ve vektörler le ilgili sorum olacak yardımcı olur musunuz?
Gönder bakalım.
Siteye bir baktım anlatım gayet iyi resimli animasyonlu örnekler var, tebrikler ana sayfama alacam geceleri okurum
Bide bişey merak ediyorum, Çembersel hızla Çembersel sürat aynı şey midir?
Çembersel demeyelim, buna çizgisel diyelim. Çembersel yörüngenin her noktasında çembere teğet olan hız vektörüne çizgisel hız, bu vektörün büyüklüğüne (yani yönü yok sadece büyüklüğü var) çizgisel sürat denir. Hız ve sürat arasındaki farkı bir okursanız daha netleşir.
hocam bı kuram ile yerçekimini yenip insanı havalandırabilirmiyiz
Uçak ve paraşüt bunu yapıyor. Akışkanların kuramları kullanılıyor bu teknolojilerde. ?
yani bir kürenin içine insanı koysak.Küreyi bir halatla merkeze bağlasak .Merkezi motorla çevirsek küre dönüp yukarı gitmek isteyecek. halatı biraz saldığımızda dahada yükselecek bu şekilde bir yerden bir yere yolculuk yapılabilirmi
Yapay uydular böyle çalışıyor. Uzaya asansör inşa etme fikri de var. İkisinde de merkezcil kuvveti hesaplamak gerekiyor.
yada çok hızlı bir motorla bu çevirmeyi yapsak bir anda halatı koparsak madde hangi hıza ulaşır.
Başlangıç değişkenlerinin değerlerini biliyorsak Newton kanunlarıyla hesaplayabiliriz.
Bir fizik öğretmeni olarak ders notlarınızı çok beğendim. Emeğinize sağlık.
Hocam bana fiziği sevmem için bir şey söyleyin ne olur
Evreni anlamak için fizik bilmemiz gerekir. Fizik öğrenmek kolay olmayabilir ama bence çok değerli.
bir çubuğa boncuk geçirip çubuğu yatayda çevirmeye başlarsak boncuklar dışarı doğru hareket ediyor. ipin ucuna taş bağlayıp yavaş yavaş çevirmeye başlayınca düşeyde cisim giderek dışa çıkıyor. ayrıca uzayda yapay yerçekimi ivmesi yaratabilmek için geminin çembersel hareket yaptırılacağı düşünülüyor. (2001 uzay macerası ve interstellar filmlerindeki uzay gemileri gibi) bunlara nasıl bir açıklama getirelim merkezkaç kuvveti düşünmessek
Merkezcil kuvvet mantığıyla çalışlıyor hepsi.
ben de biliyorum bunlar merkezcil kuvveti ile çalışıyor ama bunu öğrenciye anlaşılır kılmak içğn ne söyleyebiliriz. ayrıca bir tır ile otomobil aynı yüksek hız ile virajı alamıyor tır savrulmasa bile tork etkisi ile devriliyor ve dışa doğru o zaman o olayda da tork etkisi yok mu demeliyiz Ayrıca siteniz çok güzel yeni haberim olduğu için üzüldüm Tebrikler
helal cok iyi eger bir youtube sitesi kurarsan cok daha iyi olur bence
Çok teşekkürler gerçekten çok faydalı bir site
Çembersel hareket yapan cisim dengede değilse bunu sadece içeri çeken kuvvet varsa cisim neden merkeze doğru hareket etmez o zmn
Hızı olduğu için tam merkeze doğru hareket edemiyor. Ama merkezcil kuvvet hızın yönünü değiştiriyor.
İlk defa bu kadar güzel ve öğretici bir siteye denk geldim. Türkiye eğitim sistemi gibi ezberletici değil yani. Sizi tebrik ediyorum zihninizin açıklığı ve zihin açıcılığınız dolayısıyla. Ben şu an 12.sınıftayım. Keşke okulda da formülleri ezberletmeseler de sizin gibi mantığını öğretseler.
Sorularda ne zaman merkezcil kuvvet bazen ice doğru alınıyor bazen merkezkaç gibi disa doğru alınıyor ya bunlarin hangisi olduğunu nerden bilebiliriz
Sadece merkezcil kuvveti kullanmak lazım sorularda, hep içe doğru almak lazım yani.
Merhaba merkezkaç kuvvetini serbest cisim diyagramında gösteriyor muyuz veya cisme etki eden net kuvveti bulurken merkezkaç kuvvetini hesbab katıyor muyuz cevaplarsanız sevinirim
Hayır göstermiyoruz. Net kuvveti bulurken merkezkaç kuvveti hesaba katılmıyor.
Merhabalar ben yks’ye hazırlanan bir ögrenciyim amatör olarak çok ilgi ve sevgi ile fizikle ilgileniyorum araştırmacı kimliğim vardır ve her yerde her konuda fizik düsünen biriyim sitedeki bütün konulara baktım ve sitenizi fizik öğrenmek için şuana kadar gördüğüm en iyi site olabilir diye düsünüyorum merakım acaba üniversitede fizikle iyi bir sekilde ilgilendikten sonra sitenizde birkaç konu hakkinda paylaşimda bulunabilir miyim ? amacım insanlara ve size faydalı olmak cevaplarsaniz sevinirim
Elbette. İletişim bölümünden yazınızı gönderirseniz değerlendiririz.
Teşekkürler gerçekten çok açıklayıcı ve kfamdaki sorulara yanıt veren bir anlatım olmuş.
Üniversite sınavına hazırlanırken bu site bana çok yardımcı oluyor.Fizikle yakından ilgileniyorum.Gelişmeleri yakından takip ediyorum.Fizik formüllerinin günlük hayata uygulanması en büyük ilgi alanım.Teorik bir şeyi pratiğe dökmek gerçekten tatmin edici bir duygu.Eğer ben de burada yazar olarak bildiklerimi insanlara aktarabilirsem sevinirim.
Bu site kime ait acaba,kişiye mi yoksa bir kuruluşa mı eğer kişiye aitse fizikle alakanız nedir öğretmen misiniz ? (Ben de sınava hazırlanıyorum bu site çok faydalı oluyor cidden teşekkürlerr ??) Son olaraak iyi bir puan alırsam fizikten ziyade mühendislik seçerim diye düşünüyorum hangi mühendislik dalları fiziğe daha dayalı acaba bilginiz var mı?? :))
Hocam o kadar güzel anlatmışsınız ki tek kelimeyle ba yıl dım. Hocam YouTube kanalı açarsanız harika olur. Çok teşekkür ederim emeğinize sağlık.
Hocam merhaba. Peki bir şişe içerisindeki suyu dairesel olarak salladığımızda suyun yükselmesi ve ortasında girdap oluşması ile merkezcil kuvvetin bir ilişkisi var mıdır?
Bence vardır. Şişenin duvarları suyu içe doğru itiyor böyle girdap oluşurtururken.
Yabi merkezcil kuvvet bildiğimiz normal kuvvet farkli bisi degil. Sadece merkeze dogru olunca merkezcil diyoruz
Evet, bir çemberin merkezine doğru uygulanan kuvvete merkezcil kuvvet diyoruz.
Hocam bir araştırma yapıyorum, takıldığım yer şurası: Merkezkaç (merkezcil) kuvvetin etkisi altında kalan bir kütlenin ağırlığı azalır mı? azalırsa bu ilişki formülü nedir? Şimdiden teşekkür ederim Hocam
Düşey düzlemde çembersel hareket yazısı sorunuza cevap bulmanıza yardımcı olabilir.
evet hocam yardımcı oldu, anladığım kadarıyla kütlenin ağırlığı değişmiyor. İlginiz için teşekkür ederim… Bir çalışmam var, pratikte işe yarıyor gibi ama bunun teorik alt yapısını çözmeye çalışıyorum… Çalışmamı ilerletmem için, yani mekanizmanın tam çalışır hale getirilmesi için küçük bir atölye yapısına gereksinim var, bunu halletmeye çalışıyorum, teorik alt yapısı fizikte bazı kavramların değişmesine neden olabilir gibi ama bu teorik kısmının oluşmasında zorlandığım için sizden yardım alabilirim sanırım Hocam, ilginize tekrar teşekkür ederim.
Hocam hiç bir yerde bulamadığım bir soru var. Bir kova ve güllemiz var. Kova 3 kg ve gülle de 2 kg olsun. Bunları tarttığımızda toplamda 5 kg lık bir ağırlık olur. Fakat güllenin kova içinde yatay düzlemde dairesel bir hareket halinde olduğunda, yani kovanın tabanında değilde, çeperinde hareket ederken, bunların hepsini tekrar tartsak toplam ağırlık yine 5 kg olur mu? Gerçekten çok merak ediyorum Hocam, saygılarımla….
Kova sadece yatay düzlemdeyse ve çembersel hareket yapıyorsa, kovanın çeperi gülleyi içeri doğru iter. Eğer gülle ile kovanın kenarı temas noktasında dik ise, kova gülleyi sadece içeri iter. Düşeyde sadece yerçekimi olacağı için tartının okuyacağı ağırlık değişmez. Bu arada kovanın da dönebilmesi için bir mekanizma lazım, bir tablanın üstünde dönüyorsa sürtünme kuvveti kovayı içeri itiyor demektir.
Merkezcil [latex]kuvvet=mv^2/r = mw^2r[/latex]
r artarsa mv2/r ye göre Merkezcil kuvvet azalır, mw2r ye göre artar görünüyor
Neyi göz ardı ediyorum
Neyi sabit tutup neyi değiştiriyoruz? Eğer v (çizgisel hız sabitse), r (yarıçap) artarsa w (açısal hız) azalır, dolayısıyla her iki durumda da merkezcil ivme ve merkezcil kuvvet azalır. Eğer w (açısal hız) sabit tutulursa bu kez v (çizgisel hız) artar, dolayısıyla merkezcil ivme ve merkezcil kuvvet de artar.
Teşekkür ederim