Daha önce hareketin ne olduğunu ve hareketin temel değişkenleri olan, konum, yer değiştirme, hız ve ivme kavramlarını öğrenmiştik. (Öğrenmediysek gözden geçirmekte fayda var.) Hareketin en basit hali olan düzgün doğrusal hareketi de incelemiştik. (Buna da isterseniz bir daha bakın.) Şimdi biraz daha karmaşık bir hareket çeşidi olan bir boyutta sabit ivmeli hareket neymiş inceleyeceğiz. Bu hareket çeşidine düzgün hızlanan hareket de denir.

İvmenin vektör olduğunu biliyoruz, bu nedenle sabit ivmeli demek, hareketlinin ivmesinin büyüklüğünün ve yönünün değişmemesi anlamına geliyor. Sabit ivme, belirli bir süre içerisindeki hız değişiminin sabit olması demektir. Yani belirli bir zaman aralığında cismin hızı aynı oranda artar veya azalır. Aynı zamanda cismin sabit ivmeli hareket edebilmesi için, Newton’un ikinci kanununa göre, o cismin üzerindeki net kuvvet sabit olmalıdır. Şimdi sabit ivmeli hareketi ve hareket denklemlerini (formüllerini) incelemeye başlayalım. Bu konu dört yazıdan oluşuyor. Önce bu yazıda sabit ivmeli hareketi genel olarak inceleyeceğiz. Sonra sırasıyla düzgün hızlanan doğrusal hareket ve düzgün yavaşlayan doğrusal hareket konularını inceleyeceğiz.

Sabit ivmeli hareket örnekleri

Sorularda karşınıza düzgün hızlanan, düzgün yavaşlayan ya da önce yavaşlayıp sonra hızlanan ifadeleri çıkabilir. Bunlar anahtar kelimeler, bir boyutta sabit ivmeli hareketten bahsedildiğini anlayabilirsiniz yani. Ayrıca sorularda bir boyut yerine tek boyut sözü de kullanılabilir. Şimdi, gelelim örneklere.

Örneğin ,uzaya fırlatılan bir roket atmosferi geçene kadar belirli süre aralıklarında sabit oranda hızlanabilir. Yani eşit zaman aralıklarında hızı eşit miktarda artar. Bir tren azami (maksimum) hızına ulaşana kadar hızını sabit oranda arttırabilir veya durmak için fren yaptığında sabit zaman aralıklarında hızını sabit bir oranda azaltabilir. Bir topu yüksek bir binadan aşağı doğru serbest bıraktığımızı (ama aşağı ya da yukarı doğru hız vererek atmadığımızı) düşünelim. Topun üzerinde sadece yer çekimi kuvveti yani ağırlığı olduğundan (hava sürtünmesini ihmal edersek), yere çarpana kadar sabit bir kuvvetin etkisinde olacaktır ve düzgünce hızlanacaktır. Aynı şekilde topu yukarı attığımızda da düzgün bir şekilde yavaşlayacağını görebiliriz.

Sabit ivmeli hareketin hareket denklemleri

Hareket denklemi demek, hareket eden bir cismin konumunu , zamanın, hızın ve ivmenin bir fonksiyonu olarak yazmak demektir. Düzgün hızlanan doğrusal harekette hareket denkleminin nasıl çıkarıldığını ayrıntılı anlatacağız. Şimdilik tepeden indirip formülü vereceğiz:

Fonksiyon demek matematikte şöyle bir şey:

f(x) = ax^2+bx+c

gibi bir şey olabilir. Şimdi hareket denklemi ya da fonksiyonunu sabit ivmeli hareket için yazalım:

x(t) = x_0 + v_0t +\frac{1}{2}at^2

Şimdi bu ne demek okuyalım. Cismin herhangi bir t anındaki konumu, başlangıç konumu (x₀) artı başlangıç hızıyla (v₀) t süresinin çarpımı artı ivmesiyle (a) t süresinin karesinin (t²) çarpımının yarısına (1/2) eşittir.

Bir de hız denklemini yazalım:

v(t) = v_0 + at

Herhangi bir zamanda hareketlinin hızını bulabiliriz: İlk hızıyla (v₀) ivme (a) çarpı süreyi (t) toplamamız yeter. Böyle okuyunca pek birşey anlaşılmadı değil mi? Örnek verirsek anlaşılacak ama.

Örnek soru 1: sabit ivmeyle hızlanan araba

Doğrusal bir yolda başlangıçta trafik ışıklarında durmakta olan bir araba, yeşil ışık yanınca 3 m/s² sabit ivmeyle hızlanmaya başlıyor. Buna göre (a) araba yeşil ışık yandıktan 6 saniye sonra trafik ışıklarından kaç metre uzakta olur? (b) 6. saniyede arabanın hızı kaç m/s olur?

Çözüm:

Soru karmaşık gibi görünebilir ama aslında pek değil. Arabanın bir boyutta (yol doğrusalmış) sabit ivmeli hareket yaptığını biliyoruz. Bütün yapmamız gereken hareket denklemini yazmak:

x(t) = x_0 + v_0t +\frac{1}{2}at^2

Bizden istenen t = 6 saniye anında x(6) = kaç metre olacak. Yazalım.

x(6) = x_0 + v_0t +\frac{1}{2}a(6^2)

Arabanın başlangıç konumunun 0 m (referans noktası olan 1. trafik ışıklarının dibinde), ilk hızının 0 m/s (arabanın başlangıçta durduğunu söylemiş soru) ve ivmesinin de 3 m/s² olduğunu biliyoruz.

x_0 = 0 \space m; v_0 = 0 \space m/s; a = 3 \space m/s^2

Şimdi bu değerleri hareket denkleminde yerine koyalım:

x(6) = 0 + 0(6) +\frac{1}{2}3(6^2) x(6) =\frac{1}{2}3(6^2) = \frac{3 \times 36}{2} x(6) = 54 \space m

Yani arabanın 6. (altıncı) saniyedeki konumu 54 m. İlk konumu (trafik ışıklarının dibi) 0 m idi. Öyleyse araba trafik ışıklarından 54 m ötede olur.

Şimdi de b şıkkını çözelim. Arabanın hızı için denklemimiz şöyle:

v(t) = v_0 + at

Öyleyse çok kolay bu:

v(6) = 0 + 3(6) = 18 \space m/s

Yani arabanın 6. (altıncı) saniyedeki hızı 18 m/s olur.

Örnek soru 2: ilk konumu, ilk hızı olan ve sabit ivmeyle hızlanan araba

Bir önceki sorudaki araba hızı 24 m/s olunca sabit hızla gitmeye başlıyor. Bir sonraki trafik ışıklarını geçtikten 40 m sonra şoför tekrar gaza basıyor ve araba 4 m/s² sabit ivmeyle hızlanıyor. Buna göre (a) araba hızlanmaya başladıktan 3 saniye sonra ikinci trafik ışıklarından ne kadar uzaklıkta olur? (b) 3. saniyede arabanın hızı kaç m/s olur?

Çözüm:

Bakın bu soru daha da karmaşık gibi görünüyor. Yok ikinci ışıklar 24’ler, 40’lar, 3’ler, 4’ler falan bir sürü sayı. Öyle düşünmeyin, sakin sakin bakalım birlikte. Hareket denklemini yazalım önce, sabit ivmeli hareketin denklemi hep aynı denklem:

x(t) = x_0 + v_0t +\frac{1}{2}at^2

Bizden t = 3 s anındaki konum isteniyor. Çözmemiz gereken denklem şu yani:

x(3) = x_0 + v_0(3) +\frac{1}{2}a(3^2)

x₀, v₀ ve a değerlerini yerine koyarsak çözeriz bunu.

x_0 = 40 \space m; v_0 = 24 \space m/s; a = 4 \space m/s^2

Bunların hepsi soruda verilmiş. Referans noktasının 2. trafik ışıkları olduğuna dikkat edin. Şimdi hareket denkleminde yerine koyalım bu değerleri.

x(3) = 40 + 24 (3) +\frac{1}{2}4 (3^2) x(3) =40 + 72 + 18 = 130 \space m

Bulduk işte, araba ikinci ışıklardan mesafesi 130 m imiş.

Şimdi de b şıkkını çözelim.

v(t) = v_0 + at v(3) = 24 + 4(3) = 24 +12 = 36 \space m/s

Örnek soru 3: sabit ivmeyle yavaşlayan araba ve zamansız hız formülü

Daha önceki örneklerdeki arabanın şoförü, arabanın hızı 36 m/s olduğu anda, üçüncü trafik ışıklarının kırmızı yandığını görüyor ve frene basıyor. Frene bastığında sabit ivmeyle yavaşladığına, üçüncü ışıklara 108 m uzaklıkta olduğuna ve tam ışıkların dibinde durabildiğine göre arabanın yavaşlama ivmesi kaç m/s² dir?

Çözüm:

Bu sefer zaman verilmemiş, yer değiştirme, dolayısıyla konum verilmiş. Nasıl bulacağız ivmeyi. Korkacak bir şey yok, hareket denklemlerini yazalım.

x(t) = x_0 + v_0t +\frac{1}{2}at^2 v(t) = v_0 + at

Şimdi zamanı bilmiyoruz. Ama ilk hızı ve son hızı biliyoruz. O zaman, zaman denklemi işimize yarayabilir. Deneyelim:

v(t) = v_0 + at v(t) = 0 \space m/s; v_0 = 36 \space m/s

Sonunda durduğunu bildiğimiz için v(t) = 0. Şimdi çözelim:

0 = 36 + at at = -36

Ne ivmeyi ne süreyi bulabildik, ama ikisinin çarpımını bulduk. Bunu konum denkleminde kullanabiliriz belki.

x(t) = x_0 + v_0t +\frac{1}{2}at^2 108 = 0 +36t +\frac{1}{2}(at)t 108 = 0 +36t +\frac{1}{2}(-36)t 108 = 0 +36t -18t 108 = 18t t = \frac{108}{18} = 6 \space s

Zamanı bulduk. Artık ivme kolay, hız denklemine dönelim.

v(t) = v_0 + at at = -36 6a = -36 a = \frac{-36}{6} = -6 \space m/s^2

İvmenin işaretinin eksi olması yönünün hareket yönüne zıt olması anlamına geliyor.

Zamansız hız formülü

Şimdi bir de kısa yol gösterelim. Bu kısa yola zamansız hız denklemi ya da formülü deniyor, çünkü hızı konumun ve ivmenin fonksiyonu olarak yazabiliyoruz, ama zaman terimi bulunmuyor bu fonksiyonun içinde.

v^2 = v_0^2 + 2a(x-x_0) v = \sqrt{v_0^2 + 2a(x-x_0)}

Bu formül nereden geliyor. Biraz cebir yaparak hareket denklemlerinden türetebiliyoruz:

x = x_0 + v_0t +\frac{1}{2}at^2 v = v_0 + at

Hız denkleminin iki tarafının da karesini alalım:

v^2 = (v_0 + at)^2 v^2 = v_0^2 + 2v_0at + a^2t^2

Konum denkleminin iki tarafını da 2a ile çarpalım:

2ax = 2a(x_0 + v_0t +\frac{1}{2}at^2) 2ax = 2ax_0 + 2av_0t +2\frac{1}{2}a^2t^2 2ax - 2ax_0 = 2av_0t +a^2t^2 2a(x-x_0) = 2av_0t +a^2t^2

Şimdi bunu hız denkleminin karesi alınmış halinde yerine kolaylım:

v^2 = v_0^2 + 2a(x-x_0)

İspatımızı yaptık. Bir de özel durumdan bahsedelim:

x_0 =0; v_0 = 0 \space iken: v^2 = 2ax v = \sqrt{2ax}

Sabit ivmeli hareketin grafikleri

Bu yazı çok uzadı. Yorulmuş olmalısınız. Şimdi hızlıca grafikleri de anlatayım, sonra ayrıntısını takip eden yazılarda iyice okuyun, grafiklerin ve birbirleriyle ilişkilerinin nereden geldiklerini sindirin. Yukarıda çözdüğümüz üç örnek için sırayla konum – zaman, hız – zaman ve ivme zaman grafiklerini çizeceğiz.

Örnek soru 1: sabit ivmeyle hızlanan araba

Soruyu hatırlatayım, yukarı dönmek zorunda kalmayın.

Doğrusal bir yolda başlangıçta trafik ışıklarında durmakta olan bir araba, yeşil ışık yanınca 3 m/s² sabit ivmeyle hızlanmaya başlıyor. Buna göre (a) araba yeşil ışık yandıktan 6 saniye sonra trafik ışıklarından kaç metre uzakta olur? (b) 6. saniyede arabanın hızı kaç m/s olur?

İvme – zaman grafiği

Yukarıdaki ivme zaman grafiğinde, ivmenin 0 – 6 saniye aralığında 3 m/s² değerinde sabit olduğunu görüyoruz. Grafiğin (kırmızı çizginin eğimi 0). Kırmızı çizginin altındaki alan bize hızı veriyor. İvme – zaman grafiğinden konum – zaman grafiğine geçmemizi mümkün kılıyor.

Hız – zaman grafiği

Hız – zaman grafiğini ivme zaman grafiğinin altındaki alanı hesaplayarak bulabiliyoruz. Hız – zaman grafiğinin eğimi de ivmeyi veriyor. 18 / 6 = 3 m/s² olduğuna dikkat edin. Ayrıca hız – zaman grafiğinin altındaki alan da konumu veriyor.

Konum – zaman grafiği

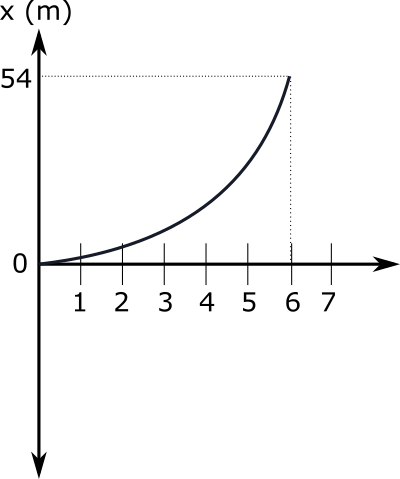
Konum – zaman grafiğini hız – zaman grafiğinin altındaki alanı hesaplayarak bulabiliyoruz. Ama dikkat edin, bu bir doğru değil, parabol (ya da ikinci dereceden bir polinom). Konum – zaman grafiğinin eğiminin artık bir sayı değil, bir fonksiyon olduğuna, bunun da hız fonksiyonu olduğuna dikkat edin. Yani konum – zaman grafiğinin eğimi hızı veriyor.

Grafikler arası geçişler

• Konum – zamanın eğimi => hız – zaman
• Hız – zamanın eğimi => ivme -zaman
• İvme -zamanın altında kalan alan => hız – zaman
• Hız – zamanın altında kalan alan => konum – zaman

Örnek soru 2: ilk konumu, ilk hızı olan ve sabit ivmeyle hızlanan araba

Bir önceki sorudaki araba hızı 24 m/s olunca sabit hızla gitmeye başlıyor. Bir sonraki trafik ışıklarını geçtikten 40 m sonra şoför tekrar gaza basıyor ve araba 4 m/s² sabit ivmeyle hızlanıyor. Buna göre (a) araba hızlanmaya başladıktan 3 saniye sonra ikinci trafik ışıklarından ne kadar uzaklıkta olur? (b) 3. saniyede arabanın hızı kaç m/s olur?

İvme – zaman grafiği

Tek fark ivme 4 m/s² olmuş, ama hala bu değerde sabit, eğim sıfır.

Hız – zaman grafiği

Bu kez hız zaman grafiğinde dikey ekseni (hız eksenini) 24 m/s ilk hızda kestiğine dikkat edin. Hala hız – zaman grafiğinin eğimi ivmeyi veriyor.

Konum – zaman grafiği

Yine parabol, tek fark x = 40 m ilk konumdan başlamış konum zaman grafiği. Hala eğimi hız denklemini veriyor.

Grafikler arası geçişler de aynı.

Örnek soru 3: sabit ivmeyle yavaşlayan araba

Daha önceki örneklerdeki arabanın şoförü, arabanın hızı 36 m/s olduğu anda, üçüncü trafik ışıklarının kırmızı yandığını görüyor ve frene basıyor. Frene bastığında sabit ivmeyle yavaşladığına, üçüncü ışıklara 108 m uzaklıkta olduğuna ve tam ışıkların dibinde durabildiğine göre arabanın yavaşlama ivmesi kaç m/s² dir?

İvme – zaman grafiği

İvme – zaman grafiğinde ivme değerinin yatay eksenin altında negatif bir değer olan -6 m/s² değerini aldığına dikkat edin, ama hala bu değerde sabit, eğim sıfır. Bunun altında kalan alan hız değişimini veriyor, hız – zaman grafiğini çizmemize olanak sağlıyor.

Hız – zaman grafiği

Bu kez hız zaman grafiğinde eğimin negatif olduğuna dikkat edin. Hala hız – zaman grafiğinin eğimi ivmeyi veriyor.

Konum – zaman grafiği

Yine parabol, tek fark bu kez zaman geçtikçe yer değiştirme azalıyor, çünkü araba yavaşlıyor. Araba hızlanırken zaman geçtikçe yer değiştirme artıyordu. Hala eğimi hız denklemini veriyor.

Bir boyutta sabit ivmeli hareket ile ilgili kazanımlar

2017 – 11.1.4.1. Bir boyutta sabit ivmeli hareketi örneklerle açıklar.

• Hareket denklemleri verilir.

2017 – 11.1.4.2. Bir boyutta sabit ivmeli hareket ile ilgili hesaplamalar yapar.

• Öğrencilerin sabit ivmeli hareket ile ilgili konum – zaman, hız – zaman ve ivme – zaman grafiklerini yorumlamaları sağlanır.