Otoyolda giden bir otobüsün içindeki insanları düşünün. Otobüsün içindeki insanlar birbirlerine göre hareket ediyorlar mı? Peki ya yol kenarında duran bir gözlemciye göre otobüsün içindeki insanlar hareket ediyorlar mı? Otobüsün içindekiler koltuklarında oturuyorlar, koltuklar da hareket etmiyor, demek ki otobüsün içinden bakan birine göre hareket etmiyorlar. Ama yol kenarındaki gözlemciye göre otobüsle birlikte içindeki yolcular da hareket ediyor. Öyleyse hangisi doğru, otobüsteki yolcular hareket ediyor mu, etmiyor mu? Bu sorunun cevabı nereden baktığınıza göre değişir, otobüsün içinden bakıyorsanız hareket etmiyorlar, otobüsün dışındaki yol kenarından bakıyorsanız hareket ediyorlar. Hareket daima göreli (bağıl) bir olgudur (doğal olaydır), yani gözlemcinin bulunduğu yere göre tanımlanır. Bir hareketlinin herhangi bir gözlem çerçevesindeki gözlemciye göre hareketine bağıl hareket, o gözlemciye göre hızına da bağıl hız denir. Bu yazıda bağıl hızın formülünün nasıl bulunduğunu göreceğiz.
Gözlem çerçevesi (referans sistemi) nedir?
Fizikte gözlem çerçevesi ya da referans sistemi gözlemci fikrine göre tanımlanır. Gözlem çerçevesi, gözlemcinin kendisiyle birlikte taşıdığı Öklit uzayıdır (korkmayın Öklit lafından). Yani gözlemciyle çakışık bir koordinat sistemi tanımlanır böylece yer ve yön gözlemciye göre belirlenebilir. Dolayısıyla gözlemciye göre konum, yer değiştirme, hız ve ivme gibi fiziksel büyüklüklerin ölçülmesi mümkün olur. Gözlem çerçevesi yalnızca gözlemcinin hareket durumuna (hızına) bağlıdır. Bağıl hareketi ve bağıl hızı anlamak için gözlem çerçevelerini kullanacağız.
Bir de yalnızca eylemsiz gözlem çerçevelerinden bahsedeceğiz. Eylemsiz gözlem çerçevesinde Newton’un hareket kanunları geçerlidir; bir cismin üzerindeki net kuvvet sıfırsa o cisim sabit hızla (aynı süratle bir doğru boyunca) hareketine devam eder ya da hareket etmez. Dolayısıyla eylemsiz gözlem çerçevelerinin hareket durumları değişmez yani hızları sabittir (sürati ve yönü değişmez).
Bağıl hareket nedir?
Bağıl, göre demektir. Bağıl hareket de bir gözlem çerçevesine göre hareket anlamına gelir. Eğer herşeyin dışında, hareketsiz (sabit), mutlak bir gözlem çerçevesi olsaydı, o zaman hareket bağıl bir olgu olmak zorunda olmazdı. Ama öyle bir gözlem çerçevesi yok, evrende herşey birbirine göre hareket ediyor. Bu birbirine göreliği anlatmak için de gözlem çerçevesi kavramını kullanıyoruz.

Şimdi otobüs örneğine geri dönelim. Yol kenarındaki gözlemcinin otobüsteki gözlemciyi nasıl gördüğünü anlamaya çalışalım: (Yukarıdaki resime dikkatlice bakalım.)
- Otobüsün dışında yol kenarında duran gözlemcinin gözlem çerçevesi yere göre hareketsiz, yani yere göre hızı sıfır.
- Otobüsün dışındaki gözlemcinin kendi gözlem çerçevesi kendisine göre hareket etmiyor.
- Otobüsün içindeki gözlemcinin gözlem çerçevesi, otobüsün dışındaki gözlemciye göre hareket ediyor (yol kenarındaki kişi otobüstekilerin ileri gittiğini görmez mi?)

Şimdi de otobüsün içindeki gözlemcinin yol kenarındaki adamı nasıl gördüğünü inceleyelim.
- Otobüsteki gözlemcinin gözlem çerçevesi de kendisine göre (otobüsün içine göre) hareket etmiyor.
- Otobüsün dışındaki gözlemcinin gözlem çerçevesi de, otobüsün içindeki gözlemciye göre hareket ediyor (yol kenarındaki kişinin geriye doğru gittiğini görmez mi?). Otobüsün içindekilerin otobüsün dışındaki gözlemcinin hangi yöne doğru hareket ettiğini gördüklerine dikkat edin.
Öyleyse bağıl hareket bir hareketlinin herhangi bir gözlem çerçevesine göre hareketi olarak tanımlanabilir. Otobüste yolcunun, yol kenarındaki gözlemcinin gözlem çerçevesine göre hareketi, o gözlem çerçevesine göre bağıl harekettir; otobüsteki yolcunun kendi gözlem çerçevesine göre hareketi (bu durumda hareket etmemesi) de onun gözlem çerçevesine göre bağıl harekettir.
Bağıl hız nedir?
Bağıl hareketi yani hareketin ancak bağıl olarak, yani bir gözlem çerçevesine göre anlaşılabileceğini gördük. Şimdi de hareket durumuna yani hıza bakalım, buna bağıl hız diyeceğiz. Otobüsteki ve yol kenarındaki gözlemci örneğimize tekrar dönelim. Otobüsün yere göre hızı +x yönünde (sağa doğru) \vec{v} olsun. Yol kenarındaki gözlemci otobüsün sağa doğru (+x yönünde) \vec{v} hızıyla gittiğini görüyor, kendi hızı ise yere göre sıfır (çünkü kendisi yere göre hareket etmiyor). Bu durum gayet açık. Ama bir de otobüsteki gözlemcinin yol kenarındaki gözlemcinin hızını nasıl gördüğüne bakalım. Otobüsteki gözlemci yol kenarındakinin sola doğru (-x yönünde) \vec{-v} hızıyla gittiğini görüyor.
Buradan varacağımız sonuç şu: Kendi gözlem çerçevenize göre (A) bir başka gözlem çerçevesinin (B) hızını (onun hızını ne kadar gördüğünüzü) bulmak için, onun hızından kendi hızınızı vektörel olarak çıkarırsınız. Matematiksel olarak bu bize bağıl hızın formülünü verir:
\vec{v_{AB}} = \vec{v_B} - \vec{v_A} \vec{v}_{gozlemciye \space gore \space gozlenenin \space bagil \space hizi} = \vec{v_{gozlenen}} - \vec{v_{gozleyen}}Yukarıdaki formülü okursak: A’dan bakıldığında B’nin hızını bulmak için (B’nin A’ya göre bağıl hızı), yerden bakıldığında B’nin hızını A’nın hızından vektörel olarak çıkarmamız gerekir. Bağıl hız = Gözlenenin hızı – gözleyenin hızı.
Yol kenarındaki adamın (A), otobüsü (B) hangi hızla gördüğünü (otobüsün yol kenarındaki adama göre bağıl hızını) bulmak için:
\vec{v_{AB}} = \vec{v} - 0 = \vec{v}Otobüsteki yolcunun (A) yol kenarındaki adamın (B) hızını ne kadar büyüklükte gördüğünü (otobüsteki gözlemciye göre yol kenarındaki adamın bağıl hızını) bulmak için:
\vec{v_{AB}} = 0 - \vec{v} = -\vec{v}Örnek soru 1: Bir boyutta bağıl hız
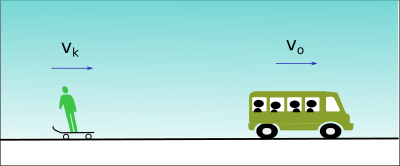
Yukarıdaki şekilde bir otobüs ve bir kaykaycı +x yönünde sırasıyla \vec{v_k} ve \vec{v_o} hızlarıyla hareket etmektedir. Bu bağıl hareket için:
- \vec{v_k} = 3 \space m/s \space ve \space \vec{v_o} = 5 \space m/s ise
a) Kaykaycıya göre otobüsün bağıl hızı hangi yönde kaç m/s’dir?
b) Otobüse göre kaykaycının bağıl hızı hangi yönde kaç m/s’dir? - \vec{v_k} = 3 \space m/s \space ve \space \vec{v_o} = 3 \space m/s ise
a) Kaykaycıya göre otobüsün bağıl hızı hangi yönde kaç m/s’dir?
b) Otobüse göre kaykaycının bağıl hızı hangi yönde kaç m/s’dir? - \vec{v_k} = 3 \space m/s \space ve \space \vec{v_o} = -5 \space m/s ise
a) Kaykaycıya göre otobüsün bağıl hızı hangi yönde kaç m/s’dir?
b) Otobüse göre kaykaycının bağıl hızı hangi yönde kaç m/s’dir?
Çözüm:
1. Bağıl hızın formülünü (aslında tanımını) öğrendik. Tek yapmamız gereken hangisi A (gözleyen) hangisi B (gözlenen) gözlem çerçevesi onu belirlemek.
\vec{v_{AB}} = \vec{v_B} - \vec{v_A}
a) bize kaykaycıya göre (A), otobüsün (B) hızı soruluyor. Öyleyse:
\vec{v_{ko}} = \vec{v_o} - \vec{v_k}
Vektörlerde çıkarma işlemini hatırlayalım, çıkarılanı ters çevirip topluyorduk.
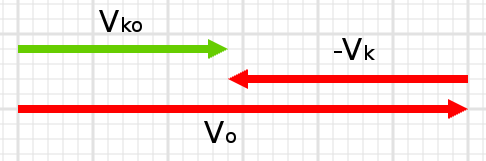
Otobüsün kaykaycıya göre bağıl hızı +x yönünde (sağa doğru) 2 m/s.
b) bize otobüse göre (A), kaykaycının (B) bağıl hızı soruluyor:
\vec{v_{ok}} = \vec{v_k} - \vec{v_o}Yine vektör çıkarması yapacağız:
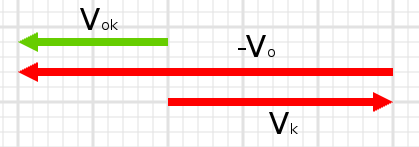
Kaykaycının otobüse göre bağıl hızı -x yönünde (sola doğru) 2 m/s.
2. Bu kez kaykaycının ve otobüsün hızları aynı yönde ve eşit büyüklükte. Vektör çıkarması yaparsak sonucun sıfır olacağı açık.
a) \vec{v}_{ko} = 3 \space m/s - 3 \space m/s = 0 \space m/s
b) \vec{v}_{ok} = 3 \space m/s - 3 \space m/s = 0 \space m/s
Yani aynı hızda aynı yöne doğru hareket eden iki araç birbirlerini duruyormuş gibi görür.
3. Bu kez otobüs kaykaycıya doğru geliyor, nereden biliyoruz, çünkü hızının -5 m/s olduğu söylenmiş, eksi işareti -x yönünde yani sola doğru hareket ediyor demek. Yine bağıl hızın tanımını kullanacağız:
\vec{v_{AB}} = \vec{v_B} - \vec{v_A}a) bize kaykaycıya göre (A), otobüsün (B) hızını soruluyor.
\vec{v_{ko}} = \vec{v_o} - \vec{v_k}
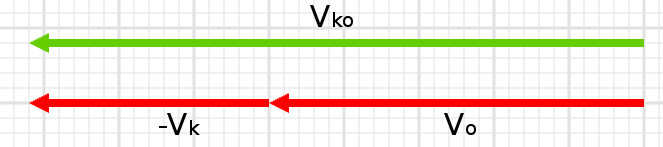
Otobüsün kaykaycıya göre bağıl hızı -x yönünde (sağa doğru) 8 m/s.
b) bize otobüse göre (A), kaykaycının (B) hızı soruluyor.
\vec{v_{ok}} = \vec{v_k} - \vec{v_o}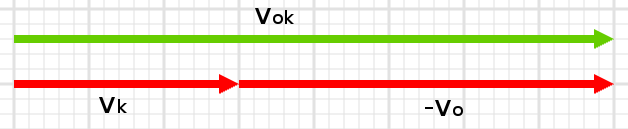
Kaykaycının otobüse göre bağıl hızı +x yönünde (sola doğru) 8 m/s.
Örnek soru 2: İki boyutta bağıl hız
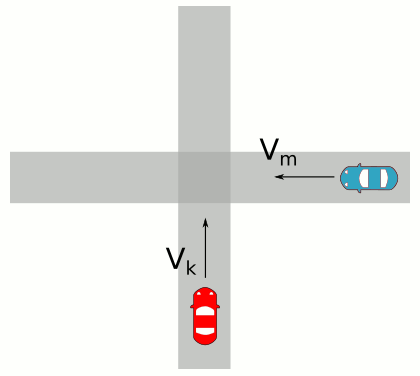
Şekildeki kırmızı araba kuzeye (+y yönüne) doğru 6 m/s, mavi araba batıya (-x yönüne) doğru 8 m/s sabit hızla hareket etmektedir. Bu bağıl hareket durumuna göre:
a) Kırmızı arabanın sürücüsü mavi arabanın hızının yönünü ne tarafa ve büyüklüğünü kaç m/s olarak görür?
b) Mavi arabanın sürücüsü kırmızı arabanın hızının yönünü hangi tarafa ve büyüklüğünü kaç m/s olarak görür?
Çözüm:
a) Kırmızı ve mavi arabaların birbirine dik doğrultularda hareket ettiklerini söylüyor soru. Bağıl hız yalnızca bir boyutta değil, iki ve üç boyutta da aynı formülle bulunur. Öyleyse vektör çıkarma işlemimizi yapalım. Kırmızı araba gözleyen, mavi araba gözlenen olduğuna göre, mavi arabanın hızından kırmızı arabanın hızını çıkaracağız:
\vec{v_{km}} = \vec{v_m} - \vec{v_k}Hız vektörlerini çizelim:
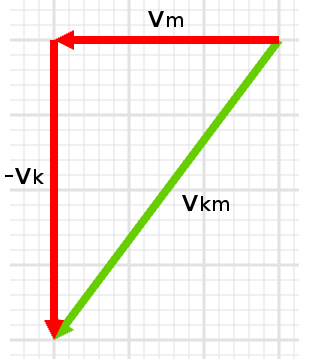
Kırmızı arabanın sürücüsü mavi arabanın güneybatıya (x ekseniyle 37° açı yaparak) gittiğini görüyor. Peki hızının büyüklüğünü (süratini) hesaplayalım şimdi:
Vektör toplamadan biliyoruz, bu bir dik üçgen ve kosinüs teoreminin özel hali olan Pisagor teoremini kullanabiliriz (isimlerden korkmayın).
v^2_{km} = v_m^2 + v_k^2Vektörlerin büyüklüklerini hesapladığımız için |-\vec{v_k}| = \sqrt {v_k^2} olduğuna dikkat edin.
\sqrt{v^2_{km}} = \sqrt{6^2 + 8^2} \sqrt{v^2_{km}} = \sqrt{36 + 64} \sqrt{v^2_{km}} = \sqrt{100} v_{km} = 10 \space m/sb) Şimdi de aynı işlemleri kırmızı arabaya bakan (gözlenen kırmızı), mavi arabanın (gözleyen mavi) sürücüsü için yapalım. Kırmızının hızından mavinin hızını vektörel olarak çıkaracağız.
\vec{v_{mk}} = \vec{v_k} - \vec{v_m}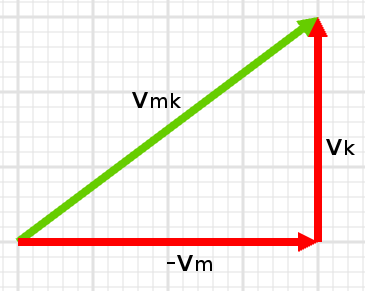
Mavi arabanın sürücüsü kırmızı arabayı kuzeydoğuya (x ekseniyle 37° açı yaparak) gidiyor görür. Hızının büyüklüğünü hesaplayalım:
v^2_{mk} = v_k^2 + v_m^2 \sqrt{v^2_{mk}} = \sqrt{8^2 + 6^2} \sqrt{v^2_{mk}} = \sqrt{64 + 36} \sqrt{v^2_{mk}} = \sqrt{100} v_{mk} = 10 \space m/sBağıl hareket ve bağıl hız ile ilgili kazanımlar
2017 – 11.1.2.1. Sabit hızlı iki cismin hareketini birbirine göre yorumlar.
2017 – 11.1.2.3. Bağıl hareket ile ilgili hesaplamalar yapar.
- Hesaplamalarla ilgili problemlerin günlük hayattan seçilmesine özen gösterilir.
bu site çok güzel herkes kullansın ulubeyden selamlar
Eğer biz ışık hızının %75i ile haraket eden bir otobüsün içindeysek ve karşımızdan aynı süratte fakat zıt yönde bir otobüs geliyorsa biz o otobüsü ışık hızının %150 si ile haraket ediyormuş gibi görürüz fakat mezo boyutlardaki hiçbir şeyin ışık hızını geçememesi gerekiyor. O zaman bu nasıl mümkün olabilir?
Özel görecelik tam bu soruyu inceliyor. Karşımızdan gelen otobüsü ışık hızının üstünde bir hızla görmemiz mümkün değil.
bağıl hız bakışı açısına göre değişen birşey eğer bakış açını 3. kişi gibi yaparsan iki otobüsünde ışık hızını geçmiyeceğini anlayabilirsi .(güzel soru)bu arada
cevabı da buldum daha basit bir örnek vereyim mesela bir tofaş var önünde maks 120 basıyor diyelim. sen tofaş maks hızla gelirken ona zıt yönde mesela 60km/h hızla gidersen tofaşı 180km/h hız yapıyor olarak görebilirsin. Işık hızını geçmek mümkün değil fakat ışık hızında giden bir araçtan ters yönde uzaklaşırsan aracın hızı daha büyük gözükür. Bu da bağıl hızın bir yanılma olduğunu kanıtlar aslında. Bu da farklı bir konu 🙂
İki araç birbirlerine göre 0,9c ile geliyor olsa birbirlerini kaç c ile geliyor gibi görürler?
1,8c mi?
Ama hiç bir şey ışık hızından daha hızlı gidemez. Nasıl olacak?
1,8c oluyor ama 1 c’yi geçemeyecekleri için ,yani ışık hızı, c ile mi görür diyeceğiz
c’den de az, hesabı yapabiliyoruz.
Merhaba, biz Fizik 1 dersinde Vmk şeklinde yazılan ifadede k nin gözlemci (referans noktası) M nin gözlenen (hesaplanan) değer olduğunu öğrendik khan academy de dahil birkaç platformla birlikte dersimize giren öğretim üyesinin slaytlarında da 2. yazılan harfin referans noktası yani gözlemci olduğu gösterildi. Yani Vmk değerini Vm-Vk şeklinde açmamız gerekiyordu yazdığınız ifadelerde hata olduğunu düşünüyorum çünkü edindiğim bilgilere göre bu sitede bir uyuşmazlık mevcut neden böyle yazıldığını öğrenebilir miyim acaba kafa karışıklığına sebebiyet veriyor da
Sadece Vmk için demeyeyim genel olarak Vgözlenen-gözlemci şeklinde yazılması gerekmez mi ifadelerin ? Yani Vab şeklinde ifade edilen değerde b gözlemci a ise gözlenen ifadedir, Vab= Va-Vb şeklinde açılmalıdır ?
Bu sadece bir gelenek meselesi. VAB birinci A’nın gözleyen, B’nin gözlenen olduğunu ifade etmek için kullanılıyor. Sonuçta asıl önemli olan gözlenenin hızından gözleyenin hızını çıkarıyor olmamız. Yoksa VAB ya da VBA daha doğru bir gösterim demek önemsiz bir ayrıntı. Önemli olan kavram.
Karanlık madde ya da karanlık enerji ismiylede bilinen.Uzayda cisimlerin belirli bir noktada cismin hareket etme ihtimali olmaz. Evrenin genişlemesini fark eden fizikçiler bu genişlemenin karanlık enerjiden öte olduğunu düşünüyorlar. Karanlık enerjinin tam olarak ne olduğu konusunda daha birşey bulmuş değiller. Evren 380 bin yaşındayken (13.7 milyar yıl önce ) karanlık madde evrende %63 tü. Geri kalanı Atomlar,fotonlar ve nötrinolardı. Ama günümüzde ise karanlık madde %23 ve 4,6 sı atomlar bunun yanı sıra %72 si karanlık enerji olmuş kısaca açıklamak gerekirse evrendeki karanlık madde miktarı azalmış ve bu azalma yüzünden karanlık enerji ortaya çıkmış peki karanlık enerji nedir?